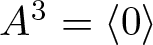A left brace is a set A with two binary operations + and · satisfying the following conditions: A is an abelian group by addition, A is a group by multiplication, and ![]() $a(b + c) = ab + ac - a$ for every
$a(b + c) = ab + ac - a$ for every ![]() $a, b, c \in A$.
$a, b, c \in A$.
In order to help study involutive set-theoretic solutions of the Yang–Baxter equation, Rump [Reference Rump5, Reference Rump6] introduced braces as a generalization of Jacobson radical rings. The main reason for introducing this algebraic object is it allowing another possible strategy to attack the problem of classifying such solutions. Subsequent papers [Reference Rump7–Reference Rump10] found connections of braces with other algebraic structures. Currently, the theory of braces is developing very intensely. An important part of this theory is the study of the internal structure of braces. One of the immediately arising questions here is the study of braces generated by one element (i.e. one-generator braces). In general, this task is very difficult, so the study of a one-generator brace should be started under some additional conditions:
Let A be a left brace. A subset S of A is called subbrace (more precisely left subbrace) if S is closed by the addition and multiplication and is the left braces by its restriction on S (i.e., S by the restriction of addition is a subgroup of an additive group of A and by the restriction of multiplication, is a subgroup of a multiplicative group of A).
Let A be a left brace. For every element ![]() $a \in A$, we define the function
$a \in A$, we define the function ![]() $\lambda_a: A \longrightarrow A$ by the rule
$\lambda_a: A \longrightarrow A$ by the rule ![]() $\lambda_a(x) = ax - a$ for all elements
$\lambda_a(x) = ax - a$ for all elements ![]() $x \in A$.
$x \in A$.
Let A be a left brace. Put ![]() $a * b = ab - a - b$. We can see that
$a * b = ab - a - b$. We can see that ![]() $a * b = \lambda_a(b) - b$. This new operation plays a very important role in left braces.
$a * b = \lambda_a(b) - b$. This new operation plays a very important role in left braces.
A left brace A is called trivial or abelian if ![]() $a * b = 0$ or
$a * b = 0$ or ![]() $a + b = ab$ for all elements
$a + b = ab$ for all elements ![]() $a, b \in A$.
$a, b \in A$.
The subbrace L of a brace A is called an ideal if ![]() $a * z, z * a \in L$ for all elements
$a * z, z * a \in L$ for all elements ![]() $a \in A$ and
$a \in A$ and ![]() $z \in L$.
$z \in L$.
If ![]() $K, L$ are subbraces of A, then denote by
$K, L$ are subbraces of A, then denote by ![]() $K * L$ the subgroup of the additive group of A generated by the elements
$K * L$ the subgroup of the additive group of A generated by the elements ![]() $x * y$, where
$x * y$, where ![]() $x \in K, y \in L$.
$x \in K, y \in L$.
Let A be the left brace. Put ![]() $A^{(1)} = A$ and, recursively,
$A^{(1)} = A$ and, recursively, ![]() $A^{(\alpha + 1)} = A^{(\alpha)} * A$ for all of ordinal α and
$A^{(\alpha + 1)} = A^{(\alpha)} * A$ for all of ordinal α and ![]() $A^{(\lambda)} = \cap_{\mu \lt \lambda} A^{(\mu)}$ for limit ordinal λ. We note that
$A^{(\lambda)} = \cap_{\mu \lt \lambda} A^{(\mu)}$ for limit ordinal λ. We note that ![]() $A^{(\alpha)}$ is an ideal of A for every ordinal α.
$A^{(\alpha)}$ is an ideal of A for every ordinal α.
A subbrace L of a left brace A is called a left ideal of A if ![]() $a * b \in L$ for every element
$a * b \in L$ for every element ![]() $a \in A$ and every element
$a \in A$ and every element ![]() $b \in L$.
$b \in L$.
Put ![]() $A^1 = A$ and, recursively,
$A^1 = A$ and, recursively, ![]() $A^{\alpha + 1} = A * A^{(\alpha)}$ for all of ordinal α and
$A^{\alpha + 1} = A * A^{(\alpha)}$ for all of ordinal α and ![]() $A^\lambda = \cap_{\mu \lt \lambda} A^\mu$ for limit ordinals λ. We note that A α is a left ideal of A for every ordinal α.
$A^\lambda = \cap_{\mu \lt \lambda} A^\mu$ for limit ordinals λ. We note that A α is a left ideal of A for every ordinal α.
Let A be a left brace and let ![]() $\mathbb{S}$ be a family of subbraces of A. Then, the intersection S of all subbraces of the family
$\mathbb{S}$ be a family of subbraces of A. Then, the intersection S of all subbraces of the family ![]() $\mathbb{S}$ is a subbrace of A. If M is the subset of A, then let
$\mathbb{S}$ is a subbrace of A. If M is the subset of A, then let ![]() $\mathbb{M}$ be the family of all subbraces of A including M. Then the intersection of all subbraces of family
$\mathbb{M}$ be the family of all subbraces of A including M. Then the intersection of all subbraces of family ![]() $\mathbb{M}$ is the least subbrace of A including M. This subbrace is called the subbrace of A generated by a subset M and will be denoted by
$\mathbb{M}$ is the least subbrace of A including M. This subbrace is called the subbrace of A generated by a subset M and will be denoted by ![]() $\mathbf{br}(M)$.
$\mathbf{br}(M)$.
A subbrace S of a brace A is called finitely generated if there exists a finite subset M such that ![]() $A = \mathbf{br}(M)$. If
$A = \mathbf{br}(M)$. If ![]() $M = \{a\}$, then A is called a one-generator brace.
$M = \{a\}$, then A is called a one-generator brace.
If ![]() $M = \{a\}$, one-generator subbrace of A.
$M = \{a\}$, one-generator subbrace of A.
One of the first basic steps pertaining to the study of left braces is the study of the one-generator braces. In general, it is a complicated problem. Every case of such study is important. In this paper, we will study one-generator braces A such that ![]() $A^3 = \langle 0 \rangle$.
$A^3 = \langle 0 \rangle$.
Like in other algebraic structures, there is the concept of nilpotency in braces. In the theory of braces, there are different approaches to this concept (see, for example, papers [Reference Cedó1–Reference Jespers, van Antwerpen and Vendramin4], [Reference Smoktunowicz11]). In the case of a one generator brace such that ![]() $A^3 = \langle 0 \rangle$, we come to the following notion of nilpotency:
$A^3 = \langle 0 \rangle$, we come to the following notion of nilpotency:
We say that A is a series that is called nilpotent in the sense of Smoktunowicz if there are positive integers ![]() $n, k$ such that
$n, k$ such that ![]() $A^{(n)} = \langle 0 \rangle = A^k$. These braces have been introduced in a paper of A. Smoktunowicz [Reference Smoktunowicz11]. Denote by
$A^{(n)} = \langle 0 \rangle = A^k$. These braces have been introduced in a paper of A. Smoktunowicz [Reference Smoktunowicz11]. Denote by ![]() $\mathcal{N}_S(n, k)$ the class of left braces satisfying
$\mathcal{N}_S(n, k)$ the class of left braces satisfying ![]() $A^{(n)} = \langle 0 \rangle = A^k$ where
$A^{(n)} = \langle 0 \rangle = A^k$ where ![]() $n, k$ are the least integers that contain this property.
$n, k$ are the least integers that contain this property.
The main results of the current paper are the following:
Theorem A. Let A be a left brace such that ![]() $A^3 = \langle 0 \rangle$. Suppose that A is generated by the element a, and put
$A^3 = \langle 0 \rangle$. Suppose that A is generated by the element a, and put ![]() $a_1 = a, a_2 = a * a = a_1 * a, a_3 = a_2 * a$. Then every element of A has a form
$a_1 = a, a_2 = a * a = a_1 * a, a_3 = a_2 * a$. Then every element of A has a form ![]() $k_1a_1 + k_2a_2 + k_3a_3$, where
$k_1a_1 + k_2a_2 + k_3a_3$, where ![]() $k_1, k_2, k_3$ are integers. Moreover, if
$k_1, k_2, k_3$ are integers. Moreover, if ![]() $x = k_1a_1 + k_2a_2 + k_3a_3, y = t_1a_1 + t_2a_2 + t_3a_3$ are elements of
$x = k_1a_1 + k_2a_2 + k_3a_3, y = t_1a_1 + t_2a_2 + t_3a_3$ are elements of ![]() $A, k_1, k_2, k_3, t_1, t_2, t_3 \in \mathbb{Z}$, then
$A, k_1, k_2, k_3, t_1, t_2, t_3 \in \mathbb{Z}$, then
 \begin{equation*}
\begin{array}{ccc}
x * y = t_1k_1a_2 + (2k_2 + k_1 - k_1^2)t_1a_3\,\mbox{and }\\
xy = (k_1 + t_1)a_1 + \frac{1}{2} (k_2 + t_2 + t_1k_1)a_2 + (k_3 + t_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1)a_3.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
x * y = t_1k_1a_2 + (2k_2 + k_1 - k_1^2)t_1a_3\,\mbox{and }\\
xy = (k_1 + t_1)a_1 + \frac{1}{2} (k_2 + t_2 + t_1k_1)a_2 + (k_3 + t_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1)a_3.
\end{array}
\end{equation*} In particular, if ![]() $a_3 = 0$, then every element of A has a form
$a_3 = 0$, then every element of A has a form ![]() $k_1a_1 + k_2a_2, k_1, k_2$ are integers. Moreover, if
$k_1a_1 + k_2a_2, k_1, k_2$ are integers. Moreover, if ![]() $x = k_1a_1 + k_2a_2, y = t_1a_1 + t_2a_2$ are elements of
$x = k_1a_1 + k_2a_2, y = t_1a_1 + t_2a_2$ are elements of ![]() $A, k_1, k_2, t_1, t_2 \in \mathbb{Z}$, then
$A, k_1, k_2, t_1, t_2 \in \mathbb{Z}$, then
Furthermore, A is nilpotent in the sense of Smoktunowicz. More precisely, ![]() $A \in \mathcal{N}_S(3, 3)$ whenever
$A \in \mathcal{N}_S(3, 3)$ whenever ![]() $a_3 = 0$, and
$a_3 = 0$, and ![]() $A \in \mathcal{N}_S(4, 3)$ whenever
$A \in \mathcal{N}_S(4, 3)$ whenever ![]() $a_3 \neq 0$.
$a_3 \neq 0$.
Theorem B1. There exists a one-generator left brace ![]() $D = \mathbb{Z} \times \mathbb{Z}$ where the addition and multiplication are defined by the rules:
$D = \mathbb{Z} \times \mathbb{Z}$ where the addition and multiplication are defined by the rules:
 \begin{equation*}
\begin{array}{ccc}
(k_1, k_2) + (t_1, t_2) = (k_1 + t_1, k_2 + t_2), \\
(k_1, k_2)(t_1, t_2) = (k_1 + t_1, k_1t_1 + k_2 + t_2).
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
(k_1, k_2) + (t_1, t_2) = (k_1 + t_1, k_2 + t_2), \\
(k_1, k_2)(t_1, t_2) = (k_1 + t_1, k_1t_1 + k_2 + t_2).
\end{array}
\end{equation*} If A is an arbitrary one-generator left brace such that ![]() $A \in \mathcal{N}_S(3, 3)$, then there exists an epimorphism
$A \in \mathcal{N}_S(3, 3)$, then there exists an epimorphism ![]() $f: D \longrightarrow A$.
$f: D \longrightarrow A$.
Theorem B2. There exists a one-generator left brace ![]() $D = \mathbb{Z} \times \mathbb{Z} \times \mathbb{Z}$ where the addition and multiplication are defined by the rules:
$D = \mathbb{Z} \times \mathbb{Z} \times \mathbb{Z}$ where the addition and multiplication are defined by the rules:
 \begin{equation*}
\begin{array}{ccc}
(k_1, k_2, k_3) + (t_1, t_2, t_3) = (k_1 + t_1, k_2 + t_2, k_3 + t_3), \\
(k_1, k_2, k_3)(t_1, t_2, t_3) = (k_1 + t_1, k_1t_1 + k_2 + t_2, k_3 + t_3 + \frac{1}{2} (2k_2 + k_1 - k_1^2)t_1).
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
(k_1, k_2, k_3) + (t_1, t_2, t_3) = (k_1 + t_1, k_2 + t_2, k_3 + t_3), \\
(k_1, k_2, k_3)(t_1, t_2, t_3) = (k_1 + t_1, k_1t_1 + k_2 + t_2, k_3 + t_3 + \frac{1}{2} (2k_2 + k_1 - k_1^2)t_1).
\end{array}
\end{equation*} If A is an arbitrary one-generator left brace such that ![]() $A \in \mathcal{N}_S(4, 3)$, then there exists an epimorphism
$A \in \mathcal{N}_S(4, 3)$, then there exists an epimorphism ![]() $f: D \longrightarrow A$.
$f: D \longrightarrow A$.
Thus, we can see that the left brace, constructed in Theorem B1 (respectively, in Theorem B2), is a free one-generator left brace such that ![]() $A^3 = \langle 0 \rangle = A^{(3)}$ (respectively,
$A^3 = \langle 0 \rangle = A^{(3)}$ (respectively, ![]() $A^3 = \langle 0 \rangle = A^{(4)})$.
$A^3 = \langle 0 \rangle = A^{(4)})$.
1. Some preliminary results
We will also need the following properties of operation * and the mapping λa. One can find the proofs of these results in papers [Reference Cedó1, Reference Jespers, van Antwerpen and Vendramin4], for example.
Lemma 1.1. Let A be a left brace. Then
 \begin{equation*}
\begin{array}{ccc}
a * (b + c) = a * b + a * c, (ab) * c = a * (b*c) + b*c + a*c,\\
(a + b)*c = a*(\lambda_{a^{-1}} (b) * c) + (\lambda_{a^{-1}} (b) * c) + a * c.\\
\lambda_y(b * a) = yby^{-1} * \lambda_y(a), yby^{-1} = \lambda_y(\lambda_b(y^{-1}) - y^{-1} + b) = \lambda_y(b * y^{-1} + b),
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
a * (b + c) = a * b + a * c, (ab) * c = a * (b*c) + b*c + a*c,\\
(a + b)*c = a*(\lambda_{a^{-1}} (b) * c) + (\lambda_{a^{-1}} (b) * c) + a * c.\\
\lambda_y(b * a) = yby^{-1} * \lambda_y(a), yby^{-1} = \lambda_y(\lambda_b(y^{-1}) - y^{-1} + b) = \lambda_y(b * y^{-1} + b),
\end{array}
\end{equation*} for all elements ![]() $a, b, c, y \in A$.
$a, b, c, y \in A$.
The following result, the proof of which is possible to find in paper [Reference Cedó1], will also be used by us.
Proposition 1.2. Let A be a left brace and L be a left ideal of A. Then ![]() $L * A$ and
$L * A$ and ![]() $A * L$ are left ideals of A. Moreover, if L is an ideal of A, then
$A * L$ are left ideals of A. Moreover, if L is an ideal of A, then ![]() $L * A$ is an ideal of A.
$L * A$ is an ideal of A.
Using Proposition 1.2, we obtain:
Proposition 1.3. Let A be a left brace. Then A α is a left ideal for each ordinal α, and ![]() $A^{(\alpha)}$ is an ideal for each ordinal α.
$A^{(\alpha)}$ is an ideal for each ordinal α.
Proposition 1.4. Let A be a left brace and suppose that ![]() $A^3 = \langle 0 \rangle$. Then
$A^3 = \langle 0 \rangle$. Then
 \begin{equation*}
\begin{array}{lll}
A^2 \textit{ is abelian. Moreover, } x * y = 0 (\textit{or } xy = x + y) \textit{ for every element } x \in A, y \in A^2,\\
(xz) * y = x * y + z * y \textit{ for every element } x, y, z \in A,\\
g^n * z = n(g * z) \textit{ for every integer } n\, \mbox{and every element } g, z \in A.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lll}
A^2 \textit{ is abelian. Moreover, } x * y = 0 (\textit{or } xy = x + y) \textit{ for every element } x \in A, y \in A^2,\\
(xz) * y = x * y + z * y \textit{ for every element } x, y, z \in A,\\
g^n * z = n(g * z) \textit{ for every integer } n\, \mbox{and every element } g, z \in A.
\end{array}
\end{equation*}Proof. The equality ![]() $A^3 = \langle 0 \rangle$ implies that
$A^3 = \langle 0 \rangle$ implies that ![]() $x * y = 0$ for every element
$x * y = 0$ for every element ![]() $x \in A$,
$x \in A$, ![]() $y \in A^2$. It follows that
$y \in A^2$. It follows that ![]() $xy = x + y$. In particular, it follows that
$xy = x + y$. In particular, it follows that ![]() $A^2 = A^{(2)}$ is abelian.
$A^2 = A^{(2)}$ is abelian.
By Lemma 1.1, for every element ![]() $x, y, z$ of A, we have:
$x, y, z$ of A, we have:
Furthermore,
Hence, ![]() $g * z + g^{-1} * z = 0$. It follows that
$g * z + g^{-1} * z = 0$. It follows that ![]() $g^{-1} * z = - g * z$. Furthermore,
$g^{-1} * z = - g * z$. Furthermore,
Using ordinary induction, we obtain that ![]() $g^n * z = n(g * z)$ for every positive integer n.
$g^n * z = n(g * z)$ for every positive integer n.
Now, let n be a negative integer. Then, ![]() $n = - k, k \gt 0$. We have
$n = - k, k \gt 0$. We have ![]() $g^n = (g^{-1})^k$. By what is proven above,
$g^n = (g^{-1})^k$. By what is proven above,
Proposition 1.5. Let A be a left brace and suppose that ![]() $A^3 = \langle 0 \rangle$. Then
$A^3 = \langle 0 \rangle$. Then
 \begin{equation*}
a^m = ma + \frac{1}{2} (m^2 - m)(a * a),
\end{equation*}
\begin{equation*}
a^m = ma + \frac{1}{2} (m^2 - m)(a * a),
\end{equation*}for every element a of A and every integer m.
Proof. Put ![]() $b = a * a$. From
$b = a * a$. From ![]() $a * a = a^2 - a - a = a^2 - 2a$, we obtain that
$a * a = a^2 - a - a = a^2 - 2a$, we obtain that ![]() $a^2 = 2a + b$. Further,
$a^2 = 2a + b$. Further,
 \begin{equation*}
\begin{array}{ccc}
a^3 = aa^2 = a(a + a + b) = a^2 + a^2 + ab - 2a = 2a + b + 2a + b + ab - 2a = \\
= 2a + 2b + ab.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
a^3 = aa^2 = a(a + a + b) = a^2 + a^2 + ab - 2a = 2a + b + 2a + b + ab - 2a = \\
= 2a + 2b + ab.
\end{array}
\end{equation*} By what is noted above, ![]() $ab = a + b$, so that
$ab = a + b$, so that ![]() $a^3 = 2a + 2b + a + b = 3a + 3b$. Again, we have:
$a^3 = 2a + 2b + a + b = 3a + 3b$. Again, we have:
 \begin{equation*}
\begin{array}{ccc}
a^4 = aa^3 = a(a + a + a + b + b + b) = 3a^2 + 3ab - 5a = \\
= 3(2a + b) + 3a + 3b - 5a = 4a + 6b,\\
a^5 = aa^4 = a(4a + 6b) = 4a^2 + 6ab - 9a = 4(2a + b) + 6a + 6b - 9a = \\
= 5a + 10b,\\
a^6 = aa^5 = a(5a + 10b) = 5a^2 + 10ab - 14a = 5(2a + b) + 10a + 10b - 14a = \\
6a + 15b.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
a^4 = aa^3 = a(a + a + a + b + b + b) = 3a^2 + 3ab - 5a = \\
= 3(2a + b) + 3a + 3b - 5a = 4a + 6b,\\
a^5 = aa^4 = a(4a + 6b) = 4a^2 + 6ab - 9a = 4(2a + b) + 6a + 6b - 9a = \\
= 5a + 10b,\\
a^6 = aa^5 = a(5a + 10b) = 5a^2 + 10ab - 14a = 5(2a + b) + 10a + 10b - 14a = \\
6a + 15b.
\end{array}
\end{equation*} Applying ordinary induction, we obtain that  $a^m = ma + \frac{1}{2}(m^2 - m)b$ for every arbitrary positive integer m.
$a^m = ma + \frac{1}{2}(m^2 - m)b$ for every arbitrary positive integer m.
Now, suppose that m < 0. Let ![]() $y = a^{-1}$. Then
$y = a^{-1}$. Then ![]() $a^m = y^t$, where
$a^m = y^t$, where ![]() $t = -m \gt 0$. By what is proven above, we have
$t = -m \gt 0$. By what is proven above, we have  $a^m = y^t = ty + \frac{1}{2} (t^2 - t)z_1$, where
$a^m = y^t = ty + \frac{1}{2} (t^2 - t)z_1$, where ![]() $z_1 = y * y = (a^{-1}) * (a^{-1})$. Using what is stated above, we obtain
$z_1 = y * y = (a^{-1}) * (a^{-1})$. Using what is stated above, we obtain ![]() $(a^{-1}) * (a^{-1}) = - (a) * (a^{-1})$. Now, we have:
$(a^{-1}) * (a^{-1}) = - (a) * (a^{-1})$. Now, we have:
 \begin{equation*}
\begin{array}{ccc}
a * (a^{-1}) = aa^{-1} - a - a^{-1} = 1 - a - a^{-1} = 0 - a - a^{-1} = - a - a^{-1},\\
(a^{-1}) * a = a^{-1}a - a - a^{-1} = - a - a^{-1},
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
a * (a^{-1}) = aa^{-1} - a - a^{-1} = 1 - a - a^{-1} = 0 - a - a^{-1} = - a - a^{-1},\\
(a^{-1}) * a = a^{-1}a - a - a^{-1} = - a - a^{-1},
\end{array}
\end{equation*} so that ![]() $a * (a^{-1}) = (a^{-1}) * a = - a * a = - b$. Hence,
$a * (a^{-1}) = (a^{-1}) * a = - a * a = - b$. Hence, ![]() $(a^{-1}) * (a^{-1}) = a * a = b$ and
$(a^{-1}) * (a^{-1}) = a * a = b$ and
 \begin{equation*}
a^m = y^t = ty + \frac{1}{2} (t^2 - t)b = t(a^{-1}) + \frac{1}{2} (t^2 - t)b.
\end{equation*}
\begin{equation*}
a^m = y^t = ty + \frac{1}{2} (t^2 - t)b = t(a^{-1}) + \frac{1}{2} (t^2 - t)b.
\end{equation*} As we have seen above, ![]() $(a^{-1}) * a = - a - a^{-1}$. On the other hand,
$(a^{-1}) * a = - a - a^{-1}$. On the other hand, ![]() $(a^{-1}) * a = -(a * a) = -b$, so that
$(a^{-1}) * a = -(a * a) = -b$, so that ![]() $- a - a^{-1} = -b$ and
$- a - a^{-1} = -b$ and ![]() $a^{-1} = b - a$. Thus,
$a^{-1} = b - a$. Thus, ![]() $t(a^{-1}) = t(b - a)$ and:
$t(a^{-1}) = t(b - a)$ and:
 \begin{equation*}
\begin{array}{ccc}
a^m = y^t = t(a^{-1}) + \frac{1}{2} (t^2 - t)b = t(b - a) + \frac{1}{2} (t^2 - t)b = t(-a) + \frac{1}{2} (t^2 + t)b =\\
(-t)a + \frac{1}{2} (t^2 + t)b = m^a + \frac{1}{2} (m^2 - m)b.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
a^m = y^t = t(a^{-1}) + \frac{1}{2} (t^2 - t)b = t(b - a) + \frac{1}{2} (t^2 - t)b = t(-a) + \frac{1}{2} (t^2 + t)b =\\
(-t)a + \frac{1}{2} (t^2 + t)b = m^a + \frac{1}{2} (m^2 - m)b.
\end{array}
\end{equation*}Proposition 1.6. Let A be a left brace and suppose that ![]() $A^3 = \langle 0 \rangle$. Then
$A^3 = \langle 0 \rangle$. Then
 \begin{equation*}
(na) * (ka) = kn(a * a) + \frac{1}{2} (n - n^2)k((a * a) * a),
\end{equation*}
\begin{equation*}
(na) * (ka) = kn(a * a) + \frac{1}{2} (n - n^2)k((a * a) * a),
\end{equation*} for every element a of A and every integer ![]() $n, k$.
$n, k$.
Proof. Put ![]() $b = a * a, c = b * a = (a * a) * a$. We have:
$b = a * a, c = b * a = (a * a) * a$. We have:
 \begin{equation*}
a^n + a^{-n} = na + \frac{1}{2} (n^2 - n)b + (-n)a + \frac{1}{2} (n^2 + n)b = n^2b.
\end{equation*}
\begin{equation*}
a^n + a^{-n} = na + \frac{1}{2} (n^2 - n)b + (-n)a + \frac{1}{2} (n^2 + n)b = n^2b.
\end{equation*} It follows that ![]() $a^n + a^{-n} - n^2b = 0$, and therefore
$a^n + a^{-n} - n^2b = 0$, and therefore ![]() $- a^n = a^{-n} - n^2b$.
$- a^n = a^{-n} - n^2b$.
Now, we will find the element ![]() $(na) * (ka)$. Using Lemma 1.1, we obtain that:
$(na) * (ka)$. Using Lemma 1.1, we obtain that: ![]() $(na) * (ka) = k((na) * a)$. Equality
$(na) * (ka) = k((na) * a)$. Equality  $a^n = na + \frac{1}{2} (n^2 - n)b$ implies that:
$a^n = na + \frac{1}{2} (n^2 - n)b$ implies that:
 \begin{equation*}
na = a^n - \frac{1}{2} (n^2 - n)b = a^n + \frac{1}{2} (n - n^2)b.
\end{equation*}
\begin{equation*}
na = a^n - \frac{1}{2} (n^2 - n)b = a^n + \frac{1}{2} (n - n^2)b.
\end{equation*}Using Proposition 1.5, we obtain that:
 \begin{equation*}
a^n + \frac{1}{2} (n - n^2)b = a^n (\frac{1}{2} (n - n^2)b).
\end{equation*}
\begin{equation*}
a^n + \frac{1}{2} (n - n^2)b = a^n (\frac{1}{2} (n - n^2)b).
\end{equation*}An application of Lemma 1.1 and Proposition 1.5 gives:
 \begin{equation*}
\begin{array}{ccc}
(na) * a = (a^n (\frac{1}{2} (n - n^2)b)) * a = a^n * a + (\frac{1}{2} (n - n^2)b) * a = \\
= n(a * a) + \frac{1}{2} (n - n^2)(b * a).
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
(na) * a = (a^n (\frac{1}{2} (n - n^2)b)) * a = a^n * a + (\frac{1}{2} (n - n^2)b) * a = \\
= n(a * a) + \frac{1}{2} (n - n^2)(b * a).
\end{array}
\end{equation*}Thus,
 \begin{equation*}
(na) * (ka) = knb + \frac{1}{2} (n - n^2)kc.
\end{equation*}
\begin{equation*}
(na) * (ka) = knb + \frac{1}{2} (n - n^2)kc.
\end{equation*}2. The structure of a one-generator brace A such that  $A^3 = \langle 0 \rangle$
$A^3 = \langle 0 \rangle$
Proposition 2.1. Let A be a left brace such that ![]() $A^3 = \langle 0 \rangle$. Let a be an element of A and put
$A^3 = \langle 0 \rangle$. Let a be an element of A and put ![]() $a_1 = a, a_2 = a * a = a_1 * a, a_3 = a_2 * a, a_{j + 1} = a_j * a, j \in \mathbb{N}$. Then the subbrace of A generated by element a is the subset of the elements having the following form:
$a_1 = a, a_2 = a * a = a_1 * a, a_3 = a_2 * a, a_{j + 1} = a_j * a, j \in \mathbb{N}$. Then the subbrace of A generated by element a is the subset of the elements having the following form: ![]() $\Sigma_{j \in \mathbb{N}} k_ja_j, k_j \in \mathbb{Z}$ and
$\Sigma_{j \in \mathbb{N}} k_ja_j, k_j \in \mathbb{Z}$ and ![]() $k_j \neq 0$ only for finitely many indices
$k_j \neq 0$ only for finitely many indices ![]() $j \in \mathbb{N}$.
$j \in \mathbb{N}$.
Proof. We note that the additive subgroup of A generated by the subset ![]() $\{a_j\: |\: j \in \mathbb{N}\}$ consists of the elements
$\{a_j\: |\: j \in \mathbb{N}\}$ consists of the elements ![]() $\Sigma_{j \in \mathbb{N}} k_ja_j$ where
$\Sigma_{j \in \mathbb{N}} k_ja_j$ where ![]() $k_j \neq 0$ only for finitely many indices j.
$k_j \neq 0$ only for finitely many indices j.
Let ![]() $x = \Sigma_{j \in \mathbb{N}} k_ja_j, y = \Sigma_{j \in \mathbb{N}} t_ja_j$. Using Lemma 1.1 and Proposition 1.4, we obtain
$x = \Sigma_{j \in \mathbb{N}} k_ja_j, y = \Sigma_{j \in \mathbb{N}} t_ja_j$. Using Lemma 1.1 and Proposition 1.4, we obtain
Proposition 1.4 implies that ![]() $\Sigma_{j \in \mathbb{N}} k_ja_j = (k_1a_j)(\Sigma_{j \gt 1} k_ja_j)$, and the fact that A 2 is abelian implies that:
$\Sigma_{j \in \mathbb{N}} k_ja_j = (k_1a_j)(\Sigma_{j \gt 1} k_ja_j)$, and the fact that A 2 is abelian implies that:
 \begin{equation*}
k_ja_j = a_j^{k_j} \mbox{for } j \gt 1, \Sigma_{j \gt 1} k_ja_j = \Pi_{j \gt 1} k_ja_j = \Pi_{j \gt 1} a_j^{k_j},
\end{equation*}
\begin{equation*}
k_ja_j = a_j^{k_j} \mbox{for } j \gt 1, \Sigma_{j \gt 1} k_ja_j = \Pi_{j \gt 1} k_ja_j = \Pi_{j \gt 1} a_j^{k_j},
\end{equation*}and we obtain,
 \begin{equation*}
\begin{array}{ccc}
x * a_1 = (\Sigma_{j \in \mathbb{N}} k_ja_j) * a_1 = (k_1a_1)(\Sigma_{j \gt 1} k_ja_j) * a_1 = (k_1a_1) * a_1 + (\Sigma_{j \gt 1} k_ja_j) * a_1 =\\
(k_1a_1) * a_1 + (\Pi_{j \gt 1} a_j^{k_j}) * a_1 = (k_1a_1) * a_1 + \Sigma_{j \gt 1} (a_j^{k_j} * a_1) =\\
(k_1a_1) * a_1 + \Sigma_{j \gt 1} k_j(a_j * a_1) = (k_1a_1) * a_1 + \Sigma_{j \gt 1} k_ja_{j + 1}.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
x * a_1 = (\Sigma_{j \in \mathbb{N}} k_ja_j) * a_1 = (k_1a_1)(\Sigma_{j \gt 1} k_ja_j) * a_1 = (k_1a_1) * a_1 + (\Sigma_{j \gt 1} k_ja_j) * a_1 =\\
(k_1a_1) * a_1 + (\Pi_{j \gt 1} a_j^{k_j}) * a_1 = (k_1a_1) * a_1 + \Sigma_{j \gt 1} (a_j^{k_j} * a_1) =\\
(k_1a_1) * a_1 + \Sigma_{j \gt 1} k_j(a_j * a_1) = (k_1a_1) * a_1 + \Sigma_{j \gt 1} k_ja_{j + 1}.
\end{array}
\end{equation*} By Proposition 1.6,  $(k_1a_1) * a_1 = k_1a_2 + \frac{1}{2} (k_1 - k_1^2)a_3$, so that:
$(k_1a_1) * a_1 = k_1a_2 + \frac{1}{2} (k_1 - k_1^2)a_3$, so that:
 \begin{equation*}
\begin{array}{ccc}
x * a_1 = k_1a_2 + \frac{1}{2} (k_1 - k_1^2)a_3 + k_2a_3 + k_3a_4 + \Sigma_{j \gt 3} k_ja_{j + 1} =\\
k_1a_2 + \frac{1}{2} (2k_2 + k_1 - k_1^2)a_3 + k_3a_4 + \Sigma_{j \gt 3} k_ja_{j + 1}.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
x * a_1 = k_1a_2 + \frac{1}{2} (k_1 - k_1^2)a_3 + k_2a_3 + k_3a_4 + \Sigma_{j \gt 3} k_ja_{j + 1} =\\
k_1a_2 + \frac{1}{2} (2k_2 + k_1 - k_1^2)a_3 + k_3a_4 + \Sigma_{j \gt 3} k_ja_{j + 1}.
\end{array}
\end{equation*}And, we have:
 \begin{equation*}
x * y = t_1 (x * a_1) = t_1k_1a_2 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1a_3 + k_3t_1a_4 + \Sigma_{j \gt 3} k_jt_1a_{j + 1}.
\end{equation*}
\begin{equation*}
x * y = t_1 (x * a_1) = t_1k_1a_2 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1a_3 + k_3t_1a_4 + \Sigma_{j \gt 3} k_jt_1a_{j + 1}.
\end{equation*} Since ![]() $x * y = xy - x - y$, we obtain:
$x * y = xy - x - y$, we obtain:
 \begin{equation*}
\begin{array}{ccc}
xy = (\Sigma_{j \in \mathbb{N}} k_ja_j)(\Sigma_{j \in \mathbb{N}} t_ja_j) =\\
t_1k_1a_2 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1a_3 + k_3t_1a_4 + \Sigma_{j \gt 3} k_jt_1a_{j + 1} + \\
+\Sigma_{j \in \mathbb{N}} k_ja_j + \Sigma_{j \in \mathbb{N}} t_ja_j =\\
(k_1 + t_1)a_1 + (k_2 + t_2 + t_1k_1)a_2 + (k_3 + t_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1)a_3 + \\
+\Sigma_{j \ge 4} (k_j + t_j + t_1k_{j - 1})a_j.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
xy = (\Sigma_{j \in \mathbb{N}} k_ja_j)(\Sigma_{j \in \mathbb{N}} t_ja_j) =\\
t_1k_1a_2 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1a_3 + k_3t_1a_4 + \Sigma_{j \gt 3} k_jt_1a_{j + 1} + \\
+\Sigma_{j \in \mathbb{N}} k_ja_j + \Sigma_{j \in \mathbb{N}} t_ja_j =\\
(k_1 + t_1)a_1 + (k_2 + t_2 + t_1k_1)a_2 + (k_3 + t_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1)a_3 + \\
+\Sigma_{j \ge 4} (k_j + t_j + t_1k_{j - 1})a_j.
\end{array}
\end{equation*}It is possible to check that:
 \begin{equation*}
\begin{array}{ccc}
x^{-1} = -k_1a_1 + (k_1^2 - k_2)a_2 + (\frac{1}{2}(2k_2 + k_1 - k_{1^{2}})k_1 - k_3)a_3 + t_3 +\\ + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1)a_3 + \Sigma_{j \ge 4} (k_1k_{j - 1} - k_j)a_j.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
x^{-1} = -k_1a_1 + (k_1^2 - k_2)a_2 + (\frac{1}{2}(2k_2 + k_1 - k_{1^{2}})k_1 - k_3)a_3 + t_3 +\\ + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1)a_3 + \Sigma_{j \ge 4} (k_1k_{j - 1} - k_j)a_j.
\end{array}
\end{equation*} Thus, we can see that the set of elements having a form ![]() $\Sigma_{j \in \mathbb{N}} k_ja_j, k_j \in \mathbb{Z}$ for all indices
$\Sigma_{j \in \mathbb{N}} k_ja_j, k_j \in \mathbb{Z}$ for all indices ![]() $j \in \mathbb{N}$ is a subbrace. On the other hand, every subbrace containing an element a contains the elements
$j \in \mathbb{N}$ is a subbrace. On the other hand, every subbrace containing an element a contains the elements ![]() $\Sigma_{j \in \mathbb{N}} k_ja_j, k_j \in \mathbb{Z}$ for all indices
$\Sigma_{j \in \mathbb{N}} k_ja_j, k_j \in \mathbb{Z}$ for all indices ![]() $j \in \mathbb{N}$. Hence, we obtain that the subbrace generated by element a coincides with the set of elements having the form
$j \in \mathbb{N}$. Hence, we obtain that the subbrace generated by element a coincides with the set of elements having the form ![]() $\Sigma_{j \in \mathbb{N}} k_ja_j, k_j \in \mathbb{Z}$ for all indices
$\Sigma_{j \in \mathbb{N}} k_ja_j, k_j \in \mathbb{Z}$ for all indices ![]() $j \in \mathbb{N}$.
$j \in \mathbb{N}$.
Proof of Theorem A
By Proposition 2.1, every element x of A has a form ![]() $x = \Sigma_{j \in \mathbb{N}} k_ja_j, k_j \in \mathbb{Z}$ for all indexes
$x = \Sigma_{j \in \mathbb{N}} k_ja_j, k_j \in \mathbb{Z}$ for all indexes ![]() $j \in \mathbb{N}$. From the proof of Proposition 2.1, we also obtain that:
$j \in \mathbb{N}$. From the proof of Proposition 2.1, we also obtain that:
 \begin{equation*}
\begin{array}{ccc}
(\Sigma_{j \in \mathbb{N}} k_ja_j)(\Sigma_{j \in \mathbb{N}} t_ja_j) =\\
t_1k_1a_2 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1a_3 + k_3t_1a_4 + \Sigma_{j \gt 3} k_jt_1a_{j + 1} + \\
+ \Sigma_{j \in \mathbb{N}} k_ja_j + \Sigma_{j \in \mathbb{N}} t_ja_j =\\
(k_1 + t_1)a_1 + (k_2 + t_2 + t_1k_1)a_2 + (k_3 + t_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1)a_3 + \\
+ \Sigma_{j \geqslant 4} (k_j + t_j + t_1k_{j - 1})a_j.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
(\Sigma_{j \in \mathbb{N}} k_ja_j)(\Sigma_{j \in \mathbb{N}} t_ja_j) =\\
t_1k_1a_2 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1a_3 + k_3t_1a_4 + \Sigma_{j \gt 3} k_jt_1a_{j + 1} + \\
+ \Sigma_{j \in \mathbb{N}} k_ja_j + \Sigma_{j \in \mathbb{N}} t_ja_j =\\
(k_1 + t_1)a_1 + (k_2 + t_2 + t_1k_1)a_2 + (k_3 + t_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1)a_3 + \\
+ \Sigma_{j \geqslant 4} (k_j + t_j + t_1k_{j - 1})a_j.
\end{array}
\end{equation*}Multiplication in A must be associative. Let
 \begin{equation*}
\begin{array}{ccc}
x = \Sigma_{j \in \mathbb{N}} k_ja_j, y = \Sigma_{j \in \mathbb{N}} t_ja_j, z = \Sigma_{j \in \mathbb{N}} s_ja_j, xy = \Sigma_{j \in \mathbb{N}} r_ja_j,\\
(xy)z = \Sigma_{j \in \mathbb{N}} m_ja_j, yz = \Sigma_{j \in \mathbb{N}} u_ja_j, x(yz) = \Sigma_{j \in \mathbb{N}} v_ja_j.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
x = \Sigma_{j \in \mathbb{N}} k_ja_j, y = \Sigma_{j \in \mathbb{N}} t_ja_j, z = \Sigma_{j \in \mathbb{N}} s_ja_j, xy = \Sigma_{j \in \mathbb{N}} r_ja_j,\\
(xy)z = \Sigma_{j \in \mathbb{N}} m_ja_j, yz = \Sigma_{j \in \mathbb{N}} u_ja_j, x(yz) = \Sigma_{j \in \mathbb{N}} v_ja_j.
\end{array}
\end{equation*}We have
 \begin{align*}
m_1 &= r_1 + s_1 = k_1 + t_1 + s_1, \\
v_1 &= k_1 + u_1 = k_1 + t_1 + s_1, \\
m_2 &= r_2 + s_2 + s_1r_1 = k_2 + t_2 + t_1k_1 + s_2 + s_1(k_1 + t_1) = \\
&= k_2 + t_2 + t_1k_1 + s_2 + s_1k_1 + s_1t_1, \\
v_2 &= k_2 + u_2 + u_1k_1 = k_2 + t_2 + s_2 + s_1t_1 + (t_1 + s_1)k_1 = \\
&= k_2 + t_2 + s_2 + s_1t_1 + t_1k_1+ s_1k_1, \\
m_3 &= r_3 + s_3 + \frac{1}{2}(2r_2 + r_1 -r_1^2)s_1 = r_3 + s_3 + r_2s_1 + \frac{1}{2} r_1s_1 - \frac{1}{2}r_1^2 s_1 =\\
&k_3 + t_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1 + s_3 + (k_2 + t_2 + t_1k_1)s_1\\ & \qquad \qquad + \frac{1}{2} (k_1 + t_1)s_1 -\\
&- \frac{1}{2} (k_1^2 + t_{1^{2}} + 2k_1t_1)s_1 = k_3 + t_3 + k_2t_1 + \frac{1}{2}k_1t_1 - \frac{1}{2}k_1^2 t_1\\ & \qquad\qquad + s_3 + k_2s_1 + \\
&+ t_2s_1+ t_1k_1s_1 + \frac{1}{2}k_1s_1 + \frac{1}{2}t_1s_1 - \frac{1}{2}k_1^2 s_1 - \frac{1}{2}t_1^2 s_1 - k_1t_1s_1 = \\
&= k_3 + t_3 + k_2t_1 + \frac{1}{2}k_1t_1 - \frac{1}{2}k_1^2 t_1 + s_3 +\\
&+ k_2s_1 + t_2s_1 + \frac{1}{2}k_1s_1 + \frac{1}{2}t_1s_1 - \frac{1}{2}k_1^2 s_1 - \frac{1}{2}t_1^2 s_1, \\
&v_3 = k_3 + u_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)u_1 = k_3 + u_3 + k_2u_1 + \frac{1}{2}k_1u_1\\ & \qquad\qquad - \frac{1}{2} k_1^2 u_1 =\\
&k_3 + t_3 + s_3 + \frac{1}{2}(2t_2 + t_1 - t_{1^{2}})s_1 + k_2t_1 + k_2s_1+ \frac{1}{2}k_1t_1 + \frac{1}{2}k_1s_1 - \\
&- \frac{1}{2}k_1^2 t_1 - \frac{1}{2}k_1^2 s_1 =
k_3 + t_3 + s_3 + t_2s_1 + \frac{1}{2}t_1s_1 - \frac{1}{2} t_1^2 s_1 + k_2t_1 + k_2s_1 + \\
&+ \frac{1}{2}k_1t_1 + \frac{1}{2}k_1s_1 - \frac{1}{2}k_1^2 t_1 - \frac{1}{2}k_1^2 s_1,\\
m_4 &= r_4 + s_4 + s_1r_3 = k_4 + t_4 + t_1k_3 + s_4 + s_1(k_3 + t_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1)) = \\
&k_4 + t_4 + t_1k_3 + s_4 + s_1k_3 + s_1t_3 + k_2s_1t_1 + \frac{1}{2} k_1s_1t_1 - \frac{1}{2} k_1^2 s_1t_1, \\
v_4 &= k_4 + u_4 + u_1k_3 = k_4 + t_4 + s_4 + s_1t_3 + (t_1 + s_1)k_3 = \\
= &k_4 + t_4 + s_4 + s_1t_3 + t_1k_3 + s_1k_3.
\end{align*}
\begin{align*}
m_1 &= r_1 + s_1 = k_1 + t_1 + s_1, \\
v_1 &= k_1 + u_1 = k_1 + t_1 + s_1, \\
m_2 &= r_2 + s_2 + s_1r_1 = k_2 + t_2 + t_1k_1 + s_2 + s_1(k_1 + t_1) = \\
&= k_2 + t_2 + t_1k_1 + s_2 + s_1k_1 + s_1t_1, \\
v_2 &= k_2 + u_2 + u_1k_1 = k_2 + t_2 + s_2 + s_1t_1 + (t_1 + s_1)k_1 = \\
&= k_2 + t_2 + s_2 + s_1t_1 + t_1k_1+ s_1k_1, \\
m_3 &= r_3 + s_3 + \frac{1}{2}(2r_2 + r_1 -r_1^2)s_1 = r_3 + s_3 + r_2s_1 + \frac{1}{2} r_1s_1 - \frac{1}{2}r_1^2 s_1 =\\
&k_3 + t_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1 + s_3 + (k_2 + t_2 + t_1k_1)s_1\\ & \qquad \qquad + \frac{1}{2} (k_1 + t_1)s_1 -\\
&- \frac{1}{2} (k_1^2 + t_{1^{2}} + 2k_1t_1)s_1 = k_3 + t_3 + k_2t_1 + \frac{1}{2}k_1t_1 - \frac{1}{2}k_1^2 t_1\\ & \qquad\qquad + s_3 + k_2s_1 + \\
&+ t_2s_1+ t_1k_1s_1 + \frac{1}{2}k_1s_1 + \frac{1}{2}t_1s_1 - \frac{1}{2}k_1^2 s_1 - \frac{1}{2}t_1^2 s_1 - k_1t_1s_1 = \\
&= k_3 + t_3 + k_2t_1 + \frac{1}{2}k_1t_1 - \frac{1}{2}k_1^2 t_1 + s_3 +\\
&+ k_2s_1 + t_2s_1 + \frac{1}{2}k_1s_1 + \frac{1}{2}t_1s_1 - \frac{1}{2}k_1^2 s_1 - \frac{1}{2}t_1^2 s_1, \\
&v_3 = k_3 + u_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)u_1 = k_3 + u_3 + k_2u_1 + \frac{1}{2}k_1u_1\\ & \qquad\qquad - \frac{1}{2} k_1^2 u_1 =\\
&k_3 + t_3 + s_3 + \frac{1}{2}(2t_2 + t_1 - t_{1^{2}})s_1 + k_2t_1 + k_2s_1+ \frac{1}{2}k_1t_1 + \frac{1}{2}k_1s_1 - \\
&- \frac{1}{2}k_1^2 t_1 - \frac{1}{2}k_1^2 s_1 =
k_3 + t_3 + s_3 + t_2s_1 + \frac{1}{2}t_1s_1 - \frac{1}{2} t_1^2 s_1 + k_2t_1 + k_2s_1 + \\
&+ \frac{1}{2}k_1t_1 + \frac{1}{2}k_1s_1 - \frac{1}{2}k_1^2 t_1 - \frac{1}{2}k_1^2 s_1,\\
m_4 &= r_4 + s_4 + s_1r_3 = k_4 + t_4 + t_1k_3 + s_4 + s_1(k_3 + t_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1)) = \\
&k_4 + t_4 + t_1k_3 + s_4 + s_1k_3 + s_1t_3 + k_2s_1t_1 + \frac{1}{2} k_1s_1t_1 - \frac{1}{2} k_1^2 s_1t_1, \\
v_4 &= k_4 + u_4 + u_1k_3 = k_4 + t_4 + s_4 + s_1t_3 + (t_1 + s_1)k_3 = \\
= &k_4 + t_4 + s_4 + s_1t_3 + t_1k_3 + s_1k_3.
\end{align*}And in general,
 \begin{equation*}
\begin{array}{lll}
m_{j + 1} = r_{j + 1} + s_{j + 1} + s_1r_j = k_{j + 1} + t_{j + 1} + s_{j + 1} + t_1k_j + s_1(k_j + t_j + t_1k_{j-1}) = \\
k_{j + 1} + t_{j + 1} + s_{j + 1} + t_1k_j + s_1k_j + s_1t_j + s_1t_1k_{j - 1}, \\
v_{j + 1} = k_{j + 1} + u_{j + 1} + u_1k_j = k_{j + 1} + t_{j + 1} + s_{j + 1} + s_1t_j + (t_1 + s_1)k_j = \\
= k_{j + 1} + t_{j + 1} + s_{j + 1} + s_1t_j + t_1k_j + s_1k_j.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lll}
m_{j + 1} = r_{j + 1} + s_{j + 1} + s_1r_j = k_{j + 1} + t_{j + 1} + s_{j + 1} + t_1k_j + s_1(k_j + t_j + t_1k_{j-1}) = \\
k_{j + 1} + t_{j + 1} + s_{j + 1} + t_1k_j + s_1k_j + s_1t_j + s_1t_1k_{j - 1}, \\
v_{j + 1} = k_{j + 1} + u_{j + 1} + u_1k_j = k_{j + 1} + t_{j + 1} + s_{j + 1} + s_1t_j + (t_1 + s_1)k_j = \\
= k_{j + 1} + t_{j + 1} + s_{j + 1} + s_1t_j + t_1k_j + s_1k_j.
\end{array}
\end{equation*} Note that if ![]() $a_j = 0$, then
$a_j = 0$, then ![]() $a_{j + 1} = a_j * a = 0$, and hence
$a_{j + 1} = a_j * a = 0$, and hence ![]() $a_{j + k} = 0$ for all positive integer k.
$a_{j + k} = 0$ for all positive integer k.
Suppose that ![]() $2a_1 \neq 0$. Then we have:
$2a_1 \neq 0$. Then we have:
 \begin{equation*}
\begin{array}{lll}
a_2a_1 = 3a_1 + 2a_2 - a_3, ((2a_1)a_1)a_1 = (3a_1 + 2a_2 - a_3)a_1 = 4a_1 + 5a_2 - 2a_3 - a_4, \\
a_1a_1 = 2a_1 + a_2, (2a_1)(a_1a_1) = (2a_1)(2a_1 + a_2) = 4a_1 + 5a_2 - 2a_3.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lll}
a_2a_1 = 3a_1 + 2a_2 - a_3, ((2a_1)a_1)a_1 = (3a_1 + 2a_2 - a_3)a_1 = 4a_1 + 5a_2 - 2a_3 - a_4, \\
a_1a_1 = 2a_1 + a_2, (2a_1)(a_1a_1) = (2a_1)(2a_1 + a_2) = 4a_1 + 5a_2 - 2a_3.
\end{array}
\end{equation*} Thus, ![]() $(2a_1)(a_1a_1) - (2a_1)(a_1a_1) = a_4$. Hence, if
$(2a_1)(a_1a_1) - (2a_1)(a_1a_1) = a_4$. Hence, if ![]() $a_4 \neq 0$, then the multiplication is not associative. It follows that, in this case,
$a_4 \neq 0$, then the multiplication is not associative. It follows that, in this case, ![]() $a_4 = 0$. Then, also,
$a_4 = 0$. Then, also, ![]() $a_5 = a_4 * a = 0$, and, furthermore,
$a_5 = a_4 * a = 0$, and, furthermore, ![]() $a_j = 0$ for all j > 5. We can see that, in this case, A is nilpotent in the sense of Smoktunowicz, and, more precisely,
$a_j = 0$ for all j > 5. We can see that, in this case, A is nilpotent in the sense of Smoktunowicz, and, more precisely, ![]() $A \in \mathcal{N}_S(4, 3)$.
$A \in \mathcal{N}_S(4, 3)$.
If we suppose that ![]() $ma_1 = 0$ for some positive integer v, then
$ma_1 = 0$ for some positive integer v, then
and ![]() $ma_k = 0$ for all of positive integer k.
$ma_k = 0$ for all of positive integer k.
Now, consider the case when ![]() $2a_1 = 0$. Then
$2a_1 = 0$. Then ![]() $2a_2 = 0$ and
$2a_2 = 0$ and ![]() $2a_k = 0$ for all of positive integer k. Thus, in this case, the additive group of A is an elementary abelian 2–group. We have:
$2a_k = 0$ for all of positive integer k. Thus, in this case, the additive group of A is an elementary abelian 2–group. We have:
 \begin{equation*}
\begin{array}{ccc}
a_2a_1 = a_1 + a_2 + a_3, (a_2a_1)a_1 = (a_1 + a_2 + a_3)a_1 = 2a_1 + 2a_2 + a_3 + a_4 = a_3 + a_4,\\
a_1a_1 = 2a_1 + a_2 = a_2, (a_2)(a_1a_1) = a_2 a_2 = 2a_2 = 0.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
a_2a_1 = a_1 + a_2 + a_3, (a_2a_1)a_1 = (a_1 + a_2 + a_3)a_1 = 2a_1 + 2a_2 + a_3 + a_4 = a_3 + a_4,\\
a_1a_1 = 2a_1 + a_2 = a_2, (a_2)(a_1a_1) = a_2 a_2 = 2a_2 = 0.
\end{array}
\end{equation*} Equality ![]() $(a_2a_1)a_1 = (a_2)(a_1a_1)$ implies that
$(a_2a_1)a_1 = (a_2)(a_1a_1)$ implies that ![]() $a_3 + a_4 = 0$ or
$a_3 + a_4 = 0$ or ![]() $a_3 = a_4$. Then
$a_3 = a_4$. Then
![]() $a_3 = a_4 = a_3 * a_1 = a_3a_1 - a_3 - a_1 = a_3. $
$a_3 = a_4 = a_3 * a_1 = a_3a_1 - a_3 - a_1 = a_3. $
It follows that
![]() $a_3a_1 = a_3 + a_1 + a_3 = 2a_3 + a_1 = a_1.$
$a_3a_1 = a_3 + a_1 + a_3 = 2a_3 + a_1 = a_1.$
The fact that by multiplication A is a group implies that ![]() $a_3 = 1 = 0$. Then, also,
$a_3 = 1 = 0$. Then, also, ![]() $a_j = 0$ for all j > 3. By Proposition 2.1, every element of A has a form
$a_j = 0$ for all j > 3. By Proposition 2.1, every element of A has a form ![]() $k_1a_1 + k_2a_2$, where
$k_1a_1 + k_2a_2$, where ![]() $k_1, k_2$ are integers. Moreover, if
$k_1, k_2$ are integers. Moreover, if ![]() $x = k_1a_1 + k_2a_2, y = t_1a_1 + t_2a_2$ are elements of
$x = k_1a_1 + k_2a_2, y = t_1a_1 + t_2a_2$ are elements of ![]() $A, k_1, k_2, t_1, t_2 \in \mathbb{Z}$, then
$A, k_1, k_2, t_1, t_2 \in \mathbb{Z}$, then
Furthermore, A is nilpotent in the sense of Smoktunowicz. More precisely, ![]() $A \in \mathcal{N}_S(3, 3)$.
$A \in \mathcal{N}_S(3, 3)$.
Proof of Theorem B2
Clearly, by addition, D is an abelian group. Furthermore, let
 \begin{equation*}
\begin{array}{ccc}
x = (k_1, k_2, k_3), y = (t_1, t_2, t_3), z = (s_1, s_2, s_3), xy = (r_1, r_2, r_3),\\
(xy)z = (m_1, m_2, m_3), yz = (u_1, u_2, u_3), x(yz) = (v_1, v_2, v_3).
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{ccc}
x = (k_1, k_2, k_3), y = (t_1, t_2, t_3), z = (s_1, s_2, s_3), xy = (r_1, r_2, r_3),\\
(xy)z = (m_1, m_2, m_3), yz = (u_1, u_2, u_3), x(yz) = (v_1, v_2, v_3).
\end{array}
\end{equation*}We have:
 \begin{equation*}
\begin{array}{lllllllllll}
m_1 = r_1 + s_1 = k_1 + t_1 + s_1,\\
v_1 = k_1 + u_1 = k_1 + t_1 + s_1, \\
m_2 = r_2 + s_2 + s_1r_1 = k_2 + t_2 + t_1k_1 + s_2 + s_1(k_1 + t_1) = \\
= k_2 + t_2 + t_1k_1 + s_2 + s_1k_1 + s_1t_1, \\
v_2 = k_2 + u_2 + u_1k_1 = k_2 + t_2 + s_2 + s_1t_1 + (t_1 + s_1)k_1 = \\
= k_2 + t_2 + s_2 + s_1t_1 + t_1k_1+ s_1k_1,\\
m_3 = r_3 + s_3 + \frac{1}{2}(2r_2 + r_1 - r_1^2)s_1 = r_3 + s_3 + r_2s_1 + \frac{1}{2} r_1s_1 - \frac{1}{2}r_1^2 s_1 =\\
k_3 + t_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1 + s_3 + (k_2 + t_2 + t_1k_1)s_1 + \frac{1}{2} (k_1 + t_1)s_1 -\\
- \frac{1}{2} (k_1^2 + t_1^2 + 2k_1t_1)s_1 =\\
k_3 + t_3 + k_2t_1 + \frac{1}{2}k_1t_1 - \frac{1}{2}k_1^2t_1 + s_3 + k_2s_1 + t_2s_1+ t_1k_1s_1 + \frac{1}{2}k_1s_1 + \\
+ \frac{1}{2}t_1s_1 - \frac{1}{2}k_1^2 s_1 - \frac{1}{2}t_1^2 s_1 -
k_1t_1s_1 = k_3 + t_3 + k_2t_1 + \frac{1}{2}k_1t_1 - \frac{1}{2}k_1^2 t_1 + s_3 + \\
+ k_2s_1 + t_2s_1 + \frac{1}{2}k_1s_1 + \frac{1}{2}t_1s_1 - \frac{1}{2}k_1^2 s_1 - \frac{1}{2}t_1^2 s_1,\\
v_3 = k_3 + u_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)u_1 = k_3 + u_3 + k_2u_1+ \frac{1}{2}k_1u_1 - \frac{1}{2} k_1^2 u_1 =\\
k_3 + t_3 + s_3 + \frac{1}{2}(2t_2 + t_1 - t_1^2)s_1 + k_2t_1 + k_2s_1+ \frac{1}{2}k_1t_1 + \\
+ \frac{1}{2}k_1s_1 - \frac{1}{2}k_1^2 t_1 - \frac{1}{2}k_1^2 s_1 =\\
k_3 + t_3 + s_3 + t_2s_1 + \frac{1}{2}t_1s_1 - \frac{1}{2} t_{1^{2}}s_1 + k_2t_1 + k_2s_1+ \frac{1}{2}k_1t_1 + \frac{1}{2}k_1s_1 - \\
- \frac{1}{2}k_1^2 t_1 -\frac{1}{2}k_1^2 s_1.
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{lllllllllll}
m_1 = r_1 + s_1 = k_1 + t_1 + s_1,\\
v_1 = k_1 + u_1 = k_1 + t_1 + s_1, \\
m_2 = r_2 + s_2 + s_1r_1 = k_2 + t_2 + t_1k_1 + s_2 + s_1(k_1 + t_1) = \\
= k_2 + t_2 + t_1k_1 + s_2 + s_1k_1 + s_1t_1, \\
v_2 = k_2 + u_2 + u_1k_1 = k_2 + t_2 + s_2 + s_1t_1 + (t_1 + s_1)k_1 = \\
= k_2 + t_2 + s_2 + s_1t_1 + t_1k_1+ s_1k_1,\\
m_3 = r_3 + s_3 + \frac{1}{2}(2r_2 + r_1 - r_1^2)s_1 = r_3 + s_3 + r_2s_1 + \frac{1}{2} r_1s_1 - \frac{1}{2}r_1^2 s_1 =\\
k_3 + t_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1 + s_3 + (k_2 + t_2 + t_1k_1)s_1 + \frac{1}{2} (k_1 + t_1)s_1 -\\
- \frac{1}{2} (k_1^2 + t_1^2 + 2k_1t_1)s_1 =\\
k_3 + t_3 + k_2t_1 + \frac{1}{2}k_1t_1 - \frac{1}{2}k_1^2t_1 + s_3 + k_2s_1 + t_2s_1+ t_1k_1s_1 + \frac{1}{2}k_1s_1 + \\
+ \frac{1}{2}t_1s_1 - \frac{1}{2}k_1^2 s_1 - \frac{1}{2}t_1^2 s_1 -
k_1t_1s_1 = k_3 + t_3 + k_2t_1 + \frac{1}{2}k_1t_1 - \frac{1}{2}k_1^2 t_1 + s_3 + \\
+ k_2s_1 + t_2s_1 + \frac{1}{2}k_1s_1 + \frac{1}{2}t_1s_1 - \frac{1}{2}k_1^2 s_1 - \frac{1}{2}t_1^2 s_1,\\
v_3 = k_3 + u_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)u_1 = k_3 + u_3 + k_2u_1+ \frac{1}{2}k_1u_1 - \frac{1}{2} k_1^2 u_1 =\\
k_3 + t_3 + s_3 + \frac{1}{2}(2t_2 + t_1 - t_1^2)s_1 + k_2t_1 + k_2s_1+ \frac{1}{2}k_1t_1 + \\
+ \frac{1}{2}k_1s_1 - \frac{1}{2}k_1^2 t_1 - \frac{1}{2}k_1^2 s_1 =\\
k_3 + t_3 + s_3 + t_2s_1 + \frac{1}{2}t_1s_1 - \frac{1}{2} t_{1^{2}}s_1 + k_2t_1 + k_2s_1+ \frac{1}{2}k_1t_1 + \frac{1}{2}k_1s_1 - \\
- \frac{1}{2}k_1^2 t_1 -\frac{1}{2}k_1^2 s_1.
\end{array}
\end{equation*} Thus, we obtain ![]() $m_1 = v_1, m_2 = v_2, m_3 = v_3$, which proves the equality
$m_1 = v_1, m_2 = v_2, m_3 = v_3$, which proves the equality ![]() $(xy)z = x(yz)$.
$(xy)z = x(yz)$.
Thus, we can see that the multiplication is associative.
The identity element is (0, 0, 0). Indeed,
 $(0,0,0)(k_{1},k_{2},k_{3})=(0+k_{1},0+0+k_{2},0+k_{3}+\frac{1}{2}
(0+0-0)k_{1})=(k_{1},k_{2},k_{3}),$
$(0,0,0)(k_{1},k_{2},k_{3})=(0+k_{1},0+0+k_{2},0+k_{3}+\frac{1}{2}
(0+0-0)k_{1})=(k_{1},k_{2},k_{3}),$
![]() $
(k_{1},k_{2},k_{3})(0,0,0)=(k_{1}+0,0+k_{2}+0,k_{3}+0+0)=(k_{1},k_{2},k_{3}).
$
$
(k_{1},k_{2},k_{3})(0,0,0)=(k_{1}+0,0+k_{2}+0,k_{3}+0+0)=(k_{1},k_{2},k_{3}).
$
If ![]() $x = (k_1, k_2a, k_3)$, then
$x = (k_1, k_2a, k_3)$, then  $x^{-1} = (-k_1, k_{1^{2}} - k_2, k_1k_2 + \frac{1}{2} (k_{1^{2}} - k_{1^{3}}) - k_3)$.
$x^{-1} = (-k_1, k_{1^{2}} - k_2, k_1k_2 + \frac{1}{2} (k_{1^{2}} - k_{1^{3}}) - k_3)$.
Finally,
 \begin{equation*}
\begin{array}{llll}
x(y + z) = (k_1, k_2, k_3) ((t_1, t_2, t_3) + (s_1, s_2, s_3)) =\\
x(y + z) = (k_1, k_2, k_3) (t_1 + s_1, t_2 + s_2, t_3 + s_3) =\\
(k_1 + t_1 + s_1, k_1(t_1 + s_1) + k_2 + t_2 + s_2, k_3 + t_3 + s_3 + \\
+ \frac{1}{2} (2k_2 + k_1 - k_1^2)(t_1 + s_1)) =\\
(k_1 + t_1 + s_1, k_1t_1 + k_1s_1 + k_2 + t_2 + s_2, k_3 + t_3 + s_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1 + \\
+ \frac{1}{2}(2k_2 + k_1 - k_1^2)s_1),
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{llll}
x(y + z) = (k_1, k_2, k_3) ((t_1, t_2, t_3) + (s_1, s_2, s_3)) =\\
x(y + z) = (k_1, k_2, k_3) (t_1 + s_1, t_2 + s_2, t_3 + s_3) =\\
(k_1 + t_1 + s_1, k_1(t_1 + s_1) + k_2 + t_2 + s_2, k_3 + t_3 + s_3 + \\
+ \frac{1}{2} (2k_2 + k_1 - k_1^2)(t_1 + s_1)) =\\
(k_1 + t_1 + s_1, k_1t_1 + k_1s_1 + k_2 + t_2 + s_2, k_3 + t_3 + s_3 + \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1 + \\
+ \frac{1}{2}(2k_2 + k_1 - k_1^2)s_1),
\end{array}
\end{equation*} \begin{equation*}
\begin{array}{llllll}
xy + xz - x = (k_1, k_2, k_3) (t_1, t_2, t_3) + (k_1, k_2, k_3)(s_1, s_2, s_3) - \\
- (k_1, k_2, k_3) = (k_1 + t_1, k_1t_1 + k_2 + t_2, k_3 + t_3 + \frac{1}{2} (2k_2 + k_1 - k_1^2)t_1) +\\
(k_1 + s_1, k_1s_1 + k_2 + s_2, k_3 + s_3 + \frac{1}{2} (2k_2 + k_1 - k_1^2)s_1) - (k_1, k_2, k_3) =\\
(k_1 + t_1, k_1t_1 + k_2 + t_2, k_3 + t_3 + \frac{1}{2} (2k_2 + k_1 - k_1^2)t_1) +\\
(s_1, k_1s_1 + s_2, s_3 + \frac{1}{2} (2k_2 + k_1 - k_1^2)s_1) - (k_1, k_2, k_3) =\\
(k_1 + t_1 + s_1, k_1t_1 + k_1s_1 + k_2 + t_2 + s_2, k_3 + t_3 + s_3 + \\
+ \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1 + \frac{1}{2}(2k_2 + k_1 -k_1^2)s_1),
\end{array}
\end{equation*}
\begin{equation*}
\begin{array}{llllll}
xy + xz - x = (k_1, k_2, k_3) (t_1, t_2, t_3) + (k_1, k_2, k_3)(s_1, s_2, s_3) - \\
- (k_1, k_2, k_3) = (k_1 + t_1, k_1t_1 + k_2 + t_2, k_3 + t_3 + \frac{1}{2} (2k_2 + k_1 - k_1^2)t_1) +\\
(k_1 + s_1, k_1s_1 + k_2 + s_2, k_3 + s_3 + \frac{1}{2} (2k_2 + k_1 - k_1^2)s_1) - (k_1, k_2, k_3) =\\
(k_1 + t_1, k_1t_1 + k_2 + t_2, k_3 + t_3 + \frac{1}{2} (2k_2 + k_1 - k_1^2)t_1) +\\
(s_1, k_1s_1 + s_2, s_3 + \frac{1}{2} (2k_2 + k_1 - k_1^2)s_1) - (k_1, k_2, k_3) =\\
(k_1 + t_1 + s_1, k_1t_1 + k_1s_1 + k_2 + t_2 + s_2, k_3 + t_3 + s_3 + \\
+ \frac{1}{2}(2k_2 + k_1 - k_1^2)t_1 + \frac{1}{2}(2k_2 + k_1 -k_1^2)s_1),
\end{array}
\end{equation*} so that ![]() $x(y + z) = xy + xz - x$.
$x(y + z) = xy + xz - x$.
This shows that D is a left brace.
Let A be an arbitrary left brace such that ![]() $A^3 = \langle 0 \rangle = A^{(4)}$. Put
$A^3 = \langle 0 \rangle = A^{(4)}$. Put ![]() $a_1 = a, a_2 = a * a = a_1 * a, a_3 = a_2 * a$. Since
$a_1 = a, a_2 = a * a = a_1 * a, a_3 = a_2 * a$. Since ![]() $A^{(3)} \neq \langle 0 \rangle$, then
$A^{(3)} \neq \langle 0 \rangle$, then ![]() $a_3 \neq 0$. By Theorem A, every element of A has a form
$a_3 \neq 0$. By Theorem A, every element of A has a form ![]() $k_1a_1 + k_2a_2 + k_3a_3$, where
$k_1a_1 + k_2a_2 + k_3a_3$, where ![]() $k_1, k_2, k_3$ are integers.
$k_1, k_2, k_3$ are integers.
Define the mapping ![]() $f: D \longrightarrow A$ by the rule
$f: D \longrightarrow A$ by the rule ![]() $f(k_1, k_2, k_3) = k_1a_1 + k_2a_2 + k_3a_3$. Using Theorem A again, we can show that f is an epimorphism.
$f(k_1, k_2, k_3) = k_1a_1 + k_2a_2 + k_3a_3$. Using Theorem A again, we can show that f is an epimorphism.
The proof of Theorem B1 is similar.
Acknowledgements
The first author is grateful for the support Isaac Newton Institute for Mathematical Sciences and the University of Edinburgh provided in the frame of LMS Solidarity Supplementary Grant Program. The authors are sincerely grateful to Professor A. Smoktunowicz for useful consultations.