Article contents
On the strong radical of certain Banach algebras
Published online by Cambridge University Press: 20 January 2009
Extract
Let A be a complex Banach algebra. By an ideal in A we mean a two-sided idealunless otherwise specified. As in (7, p. 59) by the strong radical 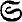 of A we mean theintersection of the modular maximal ideals of A (if there are no such ideals we set
of A we mean theintersection of the modular maximal ideals of A (if there are no such ideals we set 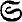 =A). Our aim is to discuss the nature of
=A). Our aim is to discuss the nature of 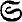 and the relation of
and the relation of 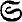 to A for a specialclass of Banach algebras. Henceforth A will denote a semi-simple modular annihilatorBanach algebra (one for which the left (right) annihilator of each modular maximalright (left) ideal is not (0)). For the theory of such algebras see (2) and (9).
to A for a specialclass of Banach algebras. Henceforth A will denote a semi-simple modular annihilatorBanach algebra (one for which the left (right) annihilator of each modular maximalright (left) ideal is not (0)). For the theory of such algebras see (2) and (9).
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1978
References
REFERENCES
- 1
- Cited by


