Published online by Cambridge University Press: 20 January 2009
Mathieu's differential equation
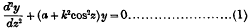
is the equation which arises out of those two-dimensional problems Mathematical Physics in which the boundary is an ellipse, such problems, for example, as the vibrations of an elliptic membrane, which was first discussed by Mathieu,* and the scattering electromagnetic waves by a wire of elliptic cross-section. A different use of the same equation is found in Celestial Mechanics the treatment of perturbations and oscillations about periodic orbits, and, in a more mundane connection, it has been shown to be the differential equation of the variety artiste who holds an assistant poised on a pole above his head while he himself is standing on a spherical ball rolling on the ground!
† Bruns : Ant. Naoh. No. 2533, S. 193-204,1883, and No. 2553, S. 129-132, 1884.
‡ Floquet: Annales de l'Eoole Normale Supérieure (2), T. 12, p. 47–88, 1883.Google Scholar
§ Hamel: Mathematische Annalen, B. 73, 8. 371-412, 1913.
* Whittaker: Cambridge International Congress, Vol. I., 1912.Google Scholar
† Hilbert: Göttingen Naohriohten, 1904, S. 213–234.Google Scholar The Hilbert integral equation is essentially different from that given by Whittaker (loc. cit.). Whittaker's has a continuous kern, whereas Hubert's kern has a discontinuity.
* Liodemann : Mathematisohe Annalen, B. 22, S. 117-123, 1883.
† Maolauriu : Trans. Camb. Phil. Soc, Vol. XVII., p. 41–108, 1899Google Scholar
* An account of this method is given in a note by Professor Whittaker in the present volume.
* Hill: Acta Mathematics, Vol. VIII., pp. 1–36, 1886.Google Scholar