No CrossRef data available.
Article contents
On the Pfaffian Invariant of a Skew-Symmetric Matrix1
Published online by Cambridge University Press: 20 January 2009
Extract
Let P be an n-rowed skew-symmetric matrix of rank 2r with elements out of an infinite field F. Denoting by x, y columns of n variables (indeterminates over F) xv, yv (v = 1, …., n), and by x′, y′ the corresponding row matrices, we consider the skew-symmetric bilinear form y′Px. It is well known that for every P a regular homogeneous substitution  over F can be found so that
over F can be found so that
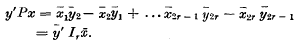
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 8 , Issue 3 , December 1949 , pp. 106 - 110
- Copyright
- Copyright © Edinburgh Mathematical Society 1949
References
page 108 note 1 Math. Annalen, 116 (1939), 620.Google Scholar
page 109 note 1 Another formal proof of the theorem was attempted by the author in an earlier note on the subject (Proc. Roy. Soc., New South Wales, 76 (1942), 177–181Google Scholar). However, a lemma upon which the proof was based turned out to be false.
page 110 note 1 Cf. Schwerdtfeger, H., American Math. Monthly, 51 (1944), 141.CrossRefGoogle Scholar


