Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Atalla, Robert
and
Sine, Robert
1976.
Random Markov mappings.
Mathematische Annalen,
Vol. 221,
Issue. 3,
p.
195.
Atalla, Robert E.
1983.
Local ergodicity of nonpositive contractions on 𝐶(𝑋).
Proceedings of the American Mathematical Society,
Vol. 88,
Issue. 3,
p.
419.
1985.
Ergodic Theorems.
p.
321.


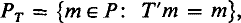 , where
, where