Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T21:53:50.097Z Has data issue: false hasContentIssue false
  • English
  • Français

On the low-dimensional cohomology groups of the IA-automorphism group of the free group of rank three

Part of: Connections with homological algebra and category theory Special aspects of infinite or finite groups

Published online by Cambridge University Press:  05 May 2021

Takao Satoh
Takao Satoh*
Affiliation:
Department of Mathematics, Faculty of Science Division II, Tokyo University of Science, 1-3, Kagurazaka, Shinjuku-ku, Tokyo162-8601, Japan ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study the structure of the rational cohomology groups of the IA-automorphism group $\mathrm {IA}_3$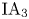 of the free group of rank three by using combinatorial group theory and representation theory. In particular, we detect a nontrivial irreducible component in the second cohomology group of $\mathrm {IA}_3$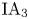, which is not contained in the image of the cup product map of the first cohomology groups. We also show that the triple cup product of the first cohomology groups is trivial. As a corollary, we obtain that the fourth term of the lower central series of $\mathrm {IA}_3$ 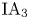has finite index in that of the Andreadakis–Johnson filtration of $\mathrm {IA}_3$.

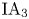Keywords

automorphism groups of free groupssecond cohomology groupsJohnson homomorphismsAndreadakis–Johnson filtration

MSC classification

Primary: 20F28: Automorphism groups of groups
Secondary: 20J06: Cohomology of groups
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 2 , May 2021 , pp. 338 - 363
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Footnotes

Dedicated to Professor Shigeyuki Morita on the occasion of his 70th birthday.

References

Andreadakis, S., On the automorphisms of free groups and free nilpotent groups, Proc. London Math. Soc. (3) 15 (1965), 239–268.CrossRefGoogle Scholar
Bachmuth, S., Induced automorphisms of free groups and free metabelian groups, Trans. Am. Math. Soc. 122 (1966), 1–17.CrossRefGoogle Scholar
Bartholdi, L., Automorphisms of free groups I, N. Y. J. Math. 19 (2013), 395–421.Google Scholar
Bartholdi, L., Erratum; Automorphisms of free groups I, N. Y. J. Math. 22 (2016), 1135–1137.Google Scholar
Bestvina, M., Bux, K.-U. and Margalit, D., Dimension of the Torelli group for $\textrm {Out} (F_n)$, Invent. Math. 170(1) (2007), 1–32.CrossRefGoogle Scholar
Brady, T., The integral cohomology of $\textrm {Out}_+ (F_3)$, J. Pure Appl. Alg. 87 (1993), 123–167.CrossRefGoogle Scholar
Cohen, F. and Pakianathan, J., On automorphism groups of free groups, and their nilpotent quotients, preprint.Google Scholar
Cohen, F. and Pakianathan, J., On subgroups of the automorphism group of a free group and associated graded Lie algebras, preprint.Google Scholar
Conant, J. and Vogtmann, K., Morita classes in the homology of automorphism groups of free groups, Geom. Topol. 8 (2004), 1471–1499.CrossRefGoogle Scholar
Conant, J., Hatcher, A., Kassabov, M. and Vogtmann, K., Assembling homology classes in automorphism groups of free groups, Comment. Math. Helv. 91(4) (2016), 751–806.CrossRefGoogle Scholar
Culler, M. and Vogtmann, K., Moduli of graphs and automorphisms of free groups, Invent. Math. 84 (1986), 91–119.CrossRefGoogle Scholar
Darné, J., On the Andreadakis problem for subgroups of the IA-group, to appear in the International Mathematical Research Notices.Google Scholar
Darné, J., On the stable Andreadakis problem, J. Pure Appl. Alg. 223(12) (2019), 5484–5525.CrossRefGoogle Scholar
Day, M. and Putman, A., On the second homology group of the Torelli subgroup of $\textrm {Aut}(F_n)$, Geom. Topol. 21(5) (2017), 2851–2896.CrossRefGoogle Scholar
Enomoto, N. and Satoh, T., On the derivation algebra of the free Lie algebra and trace maps, Alg. Geom. Top. 11 (2011), 2861–2901.CrossRefGoogle Scholar
Farb, B., Automorphisms of $F_n$ which act trivially on homology, in preparation.Google Scholar
Galatius, S., Stable homology of automorphism groups of free groups, Ann. Math. 173 (2011), 705–768.CrossRefGoogle Scholar
Gerlitz, F., Ph.D. thesis, Cornell University (2002).Google Scholar
Gersten, S. M., A presentation for the special automorphism group of a free group, J. Pure Appl. Alg. 33 (1984), 269–279.CrossRefGoogle Scholar
Hall, M., A basis for free Lie rings and higher commutators in free groups, Proc. Am. Math. Soc. 1 (1950), 575–581.CrossRefGoogle Scholar
Hall, M., The theory of groups, 2nd edn. (AMS Chelsea Publishing, 1999).Google Scholar
Hatcher, A. and Vogtmann, K., Rational homology of $\textrm {Aut}(F_n)$, Math. Res. Lett. 5 (1998), 759–780.CrossRefGoogle Scholar
Hilton, P. J. and Stammbach, U., A course in homological algebra, Graduate Texts in Mathematics, Volume 4 (Springer-Verlag, 1997).CrossRefGoogle Scholar
Kawazumi, N., Cohomological aspects of Magnus expansions, preprint, arXiv:math.GT/0505497.Google Scholar
Kontsevich, M., Formal (non)commutative symplectic geometry, in The gelfand mathematical seminars, 1990–1992, pp. 173–187 (Birkhäuser, Boston, MA, 1993).CrossRefGoogle Scholar
Kontsevich, M., Feynman diagrams and low-dimensional topology, in First European congress of mathematics, Volume II (Paris, 1992), pp. 97–121, Progress in Mathematics, Volume 120 (Birkhäuser, Basel, 1994)CrossRefGoogle Scholar
Krstić, S. and McCool, J., The non-finite presentability in $IA(F_3)$ and $GL_2(\mathbf {Z}[t,t^{-}1])$, Invent. Math. 129 (1997), 595–606.Google Scholar
Magnus, W., Über $n$-dimensinale Gittertransformationen, Acta Math. 64 (1935), 353–367.CrossRefGoogle Scholar
Magnus, W., Karras, A. and Solitar, D., Combinatorial group theory (Interscience Publishers, New York, 1966).Google Scholar
Morita, S., Structure of the mapping class groups of surfaces: a survey and a prospect, Geom. Topology Monogr. 2 (1999), 349–406.CrossRefGoogle Scholar
Morita, S., Cohomological structure of the mapping class group and beyond, Proc. Symp. Pure Math. 74 (2006), 329–354.CrossRefGoogle Scholar
Morita, S., Sakasai, T. and Suzuki, M., Computations in formal symplectic geometry and characteristic classes of moduli spaces, Quantum Topol. 6(1) (2015), 139–182.CrossRefGoogle Scholar
Nielsen, J., Die Isomorphismen der allgemeinen unendlichen Gruppe mit zwei Erzeugenden, Math. Ann. 78 (1918), 385–397.CrossRefGoogle Scholar
Nielsen, J., Die Isomorphismengruppe der freien Gruppen, Math. Ann. 91 (1924), 169–209.CrossRefGoogle Scholar
Ohashi, R., The rational homology group of $\textrm {Out}(F_n)$ for $n \leq 6$, Experiment. Math. 17(2) (2008), 167–179.CrossRefGoogle Scholar
Pettet, A., The Johnson homomorphism and the second cohomology of $IA_n$, Alg. Geom. Topology 5 (2005), 725–740.CrossRefGoogle Scholar
Reutenauer, C., Free lie algebras, London Mathematical Society Monographs, New Series, Volume 7 (Oxford University Press, 1993).Google Scholar
Satoh, T., On the Johnson homomorphisms of the mapping class groups of surfaces, in Handbook of group actions (eds. L. Ji, A. Papadopoulos and S.-T. Yau), Volume I, ALM31, pp. 373–405 (Higher Education Press and International Press, Beijing/Boston, 2015).Google Scholar
Satoh, T., New obstructions for the surjectivity of the Johnson homomorphism of the automorphism group of a free group, J. London Math. Soc. 74(2) (2006), 341–360.CrossRefGoogle Scholar
Satoh, T., The cokernel of the Johnson homomorphisms of the automorphism group of a free metabelian group, Trans. Am. Math. Soc. 361 (2009), 2085–2107.CrossRefGoogle Scholar
Satoh, T., The Johnson filtration of the McCool stabilizer subgroup of the automorphism group of a free group, Proc. Am. Math. Soc. 139 (2011), 1237–1245.CrossRefGoogle Scholar
Satoh, T., A survey of the Johnson homomorphisms of the automorphism groups of free groups and related topics, in Handbook of teichmüller theory (ed. Papadopoulos, A.), pp. 167–209, Volume V (European Mathematical Society, Zürich, Switzerland, 2016).CrossRefGoogle Scholar
Satoh, T., On the Andreadakis conjecture restricted to the “lower-triangular” IA-automorphism groups of free groups, J. Alg. Appl. 16(5) (2017), 1750099, 1–31.CrossRefGoogle Scholar
Satoh, T., The third subgroup of the Andreadakis-Johnson filtration of the automorphism group of a free group, J. Group Theory 22(1) (2019), 41–61.CrossRefGoogle Scholar
Witt, E., Treue Darstellung Liescher Ringe, J. Reine Angew. Math. 177 (1937), 152–160.Google Scholar