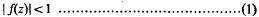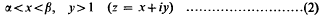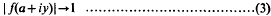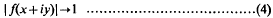Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Beardon, A. F.
1971.
Montel's theorem for subharmonic functions and solutions of partial differential equations.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 69,
Issue. 1,
p.
123.
1979.
An Introduction to Classical Complex Analysis.
Vol. 82,
Issue. ,
p.
462.
Jenkins, James A.
and
Oikawa, Kôtaro
1985.
On the boundary behavior of functions for which the Riemann image has finite spherical area.
Kodai Mathematical Journal,
Vol. 8,
Issue. 3,