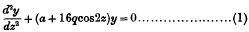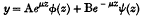Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kosirev, N. A.
1930.
Über eine Methode der Lösung von Hills Gleichung.
Astronomische Nachrichten,
Vol. 239,
Issue. 23,
p.
401.
Strutt, M. J. O.
1932.
Lamésche — Mathieusche — und Verwandte Funktionen in Physik und Technik.
p.
110.
Strutt, M. J. O.
1932.
Lamésche - Mathieusche - und Verwandte Funktionen in Physik und Technik.
p.
110.
Erdélyi, Artur
1934.
Über die freien Schwingungen in Kondensatorkreisen mit periodisch veränderlicher Kapazität.
Annalen der Physik,
Vol. 411,
Issue. 6,
p.
585.
Erdélyi, A.
1935.
Über die rechnerische Ermittlung von Schwingungsvorgängen in Kreisen mit periodisch schwankenden Parametern.
Archiv für Elektrotechnik,
Vol. 29,
Issue. 7,
p.
473.
Erdélyi, Artur
1936.
Über die Integration der Mathieuschen Differentialgleichung durch Laplacesche Integrale.
Mathematische Zeitschrift,
Vol. 41,
Issue. 1,
p.
653.
Massa, Emilio
1962.
Vibrazioni forzate e loro stabilitá in sistemi non lineari a due gradi di libertá.
Rendiconti del Seminario Matematico e Fisico di Milano,
Vol. 32,
Issue. 1,
p.
1.
Wright, I.
and
Morsztyn, K.
1970.
Subharmonic Oscillations in Power Systems-Theory and Practice.
IEEE Transactions on Power Apparatus and Systems,
Vol. PAS-89,
Issue. 8,
p.
1805.
Smith, Donald R.
1975.
The Multivariable Method in Singular Perturbation Analysis.
SIAM Review,
Vol. 17,
Issue. 2,
p.
221.
Droubi, G.
and
Sadek, M. M.
1975.
Proceedings of the Fifteenth International Machine Tool Design and Research Conference.
p.
259.
Ho, C.-H.
Scott, R.A.
and
Eisley, J.G.
1975.
Non-planar, non-linear oscillations of a beam—I. Forced motions.
International Journal of Non-Linear Mechanics,
Vol. 10,
Issue. 2,
p.
113.
Gaumond, Charles F.
and
Jacobsen, E. H.
1980.
Analysis of phonon echoes in simple insulators by means of Mathieu's equation.
Physical Review B,
Vol. 22,
Issue. 6,
p.
3001.
2000.
Perturbation Methods.
p.
387.
Frenkel, D
and
Portugal, R
2001.
Algebraic methods to compute Mathieu functions.
Journal of Physics A: Mathematical and General,
Vol. 34,
Issue. 17,
p.
3541.
Luo, Albert C.J.
2004.
Chaotic motion in the resonant separatrix bands of a Mathieu–Duffing oscillator with a twin-well potential.
Journal of Sound and Vibration,
Vol. 273,
Issue. 3,
p.
653.
Vallette, Alexandre
and
Indelicato, P.
2010.
Analytical study of electrostatic ion beam traps.
Physical Review Special Topics - Accelerators and Beams,
Vol. 13,
Issue. 11,
Rao, J. S.
2011.
History of Rotating Machinery Dynamics.
Vol. 20,
Issue. ,
p.
185.
Luo, Albert C. J.
2012.
Global Analysis of Nonlinear Dynamics.
p.
189.
Buhucianu, Ovidiu
Dariescu, Marina-Aura
and
Dariescu, Ciprian
2012.
Relativistic Bosons in Time-Harmonic Electric Fields.
International Journal of Theoretical Physics,
Vol. 51,
Issue. 2,
p.
526.
2014.
Analytical Routes to Chaos in Nonlinear Engineering.
p.
261.