No CrossRef data available.
Article contents
On the continued fractions which represent the functions of Hermite and other functions defined by differential equations
Published online by Cambridge University Press: 20 January 2009
Extract
The functions of Hermite, which are the same as the functions associated with the parabolic cylinder in harmonic analysis, may be defined* by the differential equation which they satisfy, namely,
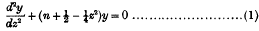
where n denotes any constant.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1913
References
* Cf. Hermite, , Comples Sendus 58 (1864), pp. 93, 266.Google Scholar
Whittker, , Proc. Load. Math. Soc. 35 (1903), p. 417.Google Scholar
Myller-Lebedeff, , Math. Ann. 64 (1907), p. 388.CrossRefGoogle Scholar
Watson, , Proc. Land. Math. Soc. (2) 8 (1910), p. 393.CrossRefGoogle Scholar
Curzon, , Proc. Load. Math. Soc. (2) 12 (1912), p. 236.Google Scholar
* Cf. a paper by the present writer in Bull. Amir. Math. Soc. (2) 10 (1903), p. 126.Google Scholar


