Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T20:30:12.126Z Has data issue: false hasContentIssue false
  • English
  • Français

On the blow-up and positive entire solutions of semilinear elliptic equations

Published online by Cambridge University Press:  20 January 2009

Jann-Long Chern
Jann-Long Chern
Affiliation:
Department of Mathematics, National Central University, Chung-Li, Taiwan 320, Republic of China ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we consider the following semilinear elliptic equation

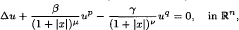
where n ≥ 3, 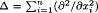and β ≥ 0, γ ≥ 0, q > p ≥ 1, μ and ν are real constants. We note that if γ = 0, β > 0 and ν ≥ 2, then the equation above is called the Matukuma-type equation. If β = 0, γ > 0 and ν > 2, then the complete classification of all possible positive solutions had been conducted by Cheng and Ni. If β > 0, γ > 0 and μ ≥ ν ≥ 2, then some results about the maximal solution and positive solution structures can be found in Chern. The purpose of this paper is to discuss and investigate the blow-up and positive entire solutions of the equation above for the μ ≥ 2 ≥ ν case.

Keywords

semilinear elliptic equationsblow-upentire solutions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 43 , Issue 3 , October 2000 , pp. 625 - 631
Copyright
Copyright © Edinburgh Mathematical Society 2000

References

1.Cheng, K.-S. and Chern, J.-L., Existence of positive solutions of some semilinear elliptic equations, J. Diff. Eqns 98 (1992), 169–180.CrossRefGoogle Scholar
2.Cheng, K.-S. and Lin, J.-T., On the elliptic equations Δu = K(x)uσ and Δu = K(x)e2u, Trans. Am. Math. Soc. 304 (1987), 639–668.Google Scholar
3.Cheng, K.-S. and Lin, T.-C., The structure of solutions of a semilinear elliptic equation, Trans. Am. Math. Soc. 332 (1992), 535–554.CrossRefGoogle Scholar
4.Cheng, K.-S. and Ni, W.-M., On the structure of the conformal scalar curvature equation on ℝn, Indiana Univ. Math. J. 41 (1992), 261–278.CrossRefGoogle Scholar
5.Chern, J.-L., On the solution structures of the semilinear elliptic equations on ℝn, Non-linear Analysis TMA, 28 (1997), 1741–1750.CrossRefGoogle Scholar
6.Gilbarg, D. and Trudinger, N. S., Elliptic partial differential equations of second order, 2nd edn, Grundlehren Math. Wiss. 224 (Springer, Berlin, 1983).Google Scholar
7.Li, Y. and Ni, W.-M., On conformal scalar curvature equations in ℝn, Duke Math. J. 57 (1988), 895–924.CrossRefGoogle Scholar
8.Matukuma, T., Dynamics of globular clusters, Nippon Temmongakkai Toho 1 (1930), 68–89.Google Scholar
9.Naito, M., A note on bounded positive entire solutions of semilinear elliptic equations, Hiroshima Math. J. 14 (1984), 211–214.CrossRefGoogle Scholar
10.Ni, W.-M., On the elliptic equation , its generalization, and applications in geometry, Indiana Univ. Math. J. 31 (1982), 493–529.CrossRefGoogle Scholar
11.Ni, W.-M. and Yotsutani, S., Semilinear elliptic equations of Matukuma-type and related topics, Japan J. Appl. Math. 5 (1988), 1–32.CrossRefGoogle Scholar
12.Yanagida, E., Structure of positive radial solutions of Matukuma's equation, Japan J. Indust. Appl. Math. 8 (1991), 165–173.CrossRefGoogle Scholar
13.Yanagida, E. and Yotsutani, S., Classification of the structure of positive radial solutions to Δ + K(|x|)up = 0 in ℝn, Arch. Ration. Mech. Analysis 124 (1993), 239–259.CrossRefGoogle Scholar