Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bogley, William A.
and
Parker, Forrest W.
2018.
Cyclically presented groups with length four positive relators.
Journal of Group Theory,
Vol. 21,
Issue. 5,
p.
911.
Bogley, William A.
Edjvet, Martin
and
Williams, Gerald
2019.
Groups St Andrews 2017 in Birmingham.
p.
169.
Aldwaik, Suzana
Edjvet, Martin
and
Juhász, Arye
2019.
Asphericity of positive free product length 4 relative group presentations.
Forum Mathematicum,
Vol. 31,
Issue. 1,
p.
49.
Edjvet, Martin
and
Eljamel, Noha
2019.
Asphericity and finiteness for certain group presentations.
Journal of Algebra,
Vol. 536,
Issue. ,
p.
39.


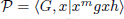 for
for 