Article contents
On the Absolute Summability (A) of Infinite Series
Published online by Cambridge University Press: 20 January 2009
Extract
§1. A series

has been defined by J. M. Whittaker to be absolutely summable (A), if

is convergent in (0 ≤ x < 1) and f (x) is of bounded variation in (0, 1), i.e.
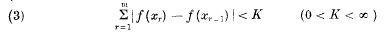
for all subdivisions 0 = x0 < x1 < x2 < . … < xm < 1.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1932
References
page 132 note 1 Proc. Edinburgh Math. Soc., (2), 2 (1930), 1–5, p. 1.CrossRefGoogle Scholar
page 132 note 2 L.c. 1, pp. 1, 2.
page 132 note 3 Fekete, , Math, és termész. ért., 29 (1911), 719–726, p. 719.Google Scholar Similarly (1) is said be absolutely summable (H, r), if the sequence ![]() of its Hölder-sums
of its Hölder-sums ![]() of order
of order ![]() is of bounded variation; Fekete, , Math, és termész. ért., 32 (1914), 389–425, p. 392.Google Scholar
is of bounded variation; Fekete, , Math, és termész. ért., 32 (1914), 389–425, p. 392.Google Scholar
page 133 note 1 L.c. 3, p. 721.
page 133 note 2 L.c. 3, pp. 397, 398.
page 133 note 3 Conversely, the existence of the integral on the left of (6) involves the absolute convergence of (4). For from the equality (7) follows the inequality

page 134 note 1 If αn and βn are positive, ![]() provided that
provided that ![]() converge in (0 ≤ x < 1), the limit on the right exists and
converge in (0 ≤ x < 1), the limit on the right exists and ![]() (CfHobson, , Theory of Functions of a Real Variable, 2 (1926), 175–177.)Google Scholar Apply Cesàro's theorem for
(CfHobson, , Theory of Functions of a Real Variable, 2 (1926), 175–177.)Google Scholar Apply Cesàro's theorem for ![]() .
.
page 134 note 2 This example is due to H. Bohr. CfLandau, , Darstellung u. Begrundüng einiger neuerer Ergebnisae der Funktionentheorie (1929), § 7, p, 51.Google Scholar
- 7
- Cited by


