Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-07T23:16:36.020Z Has data issue: false hasContentIssue false
  • English
  • Français

On Structure Groups of Set-Theoretic Solutions to the Yang–Baxter Equation

Part of: Other generalizations of groups Ordered structures Hopf algebras, quantum groups and related topics

Published online by Cambridge University Press:  11 January 2019

Victoria Lebed  and
Leandro Vendramin
Victoria Lebed
Affiliation:
Hamilton Mathematics Institute and School of Mathematics, Trinity College, Dublin 2, Ireland ([email protected]; [email protected])
Leandro Vendramin
Affiliation:
Departamento de Matemática – FCEN, Universidad de Buenos Aires, Pab. I – Ciudad Universitaria (1428), Buenos Aires, Argentina ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

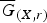This paper explores the structure groups G(X,r) of finite non-degenerate set-theoretic solutions (X,r) to the Yang–Baxter equation. Namely, we construct a finite quotient $\overline {G}_{(X,r)}$ of G(X,r), generalizing the Coxeter-like groups introduced by Dehornoy for involutive solutions. This yields a finitary setting for testing injectivity: if X injects into G(X,r), then it also injects into $\overline {G}_{(X,r)}$. We shrink every solution to an injective one with the same structure group, and compute the rank of the abelianization of G(X,r). We show that multipermutation solutions are the only involutive solutions with diffuse structure groups; that only free abelian structure groups are bi-orderable; and that for the structure group of a self-distributive solution, the following conditions are equivalent: bi-orderable, left-orderable, abelian, free abelian and torsion free.

Keywords

Yang–Baxter equationstructure groupstructure rackbijective 1-cocyclebirackquandlebiquandleinjective solutionmultipermutation solutiondiffuse grouporderable groupabelianization

MSC classification

Primary: 16T25: Yang-Baxter equations
Secondary: 20N02: Sets with a single binary operation (groupoids) 06F15: Ordered groups
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 62 , Issue 3 , August 2019 , pp. 683 - 717
Copyright
Copyright © Edinburgh Mathematical Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Andruskiewitsch, N. and Graña, M., From racks to pointed Hopf algebras, Adv. Math. 178(2) (2003), 177–243.Google Scholar
2.Bachiller, D., Cedó, F., Jespers, E. and Okniński, J., A family of irretractable square-free solutions of the Yang–Baxter equation, Forum Math. 29(6) (2017), 1291–1306.Google Scholar
3.Bachiller, D., Cedó, F. and Vendramin, L., A characterization of finite multipermutation solutions of the Yang–Baxter equation, Publ. Math. 62(6) (2018), 641–649.Google Scholar
4.Brieskorn, E., Automorphic sets and braids and singularities, in Braids (Santa Cruz, CA, 1986), Contemporary Mathematics, Volume 78, pp. 45–115 (American Mathematical Society, Providence, RI, 1988).Google Scholar
5.Cedó, F., Gateva-Ivanova, T. and Smoktunowicz, A., On the Yang–Baxter equation and left nilpotent left braces, J. Pure Appl. Algebra 221 (2017), 751–756.Google Scholar
6.Cedó, F., Jespers, E. and del Río, Á., Involutive Yang–Baxter groups, Trans. Amer. Math. Soc. 362(5) (2010), 2541–2558.Google Scholar
7.Cedó, F., Jespers, E. and Okniński, J., Retractability of set theoretic solutions of the Yang–Baxter equation, Adv. Math. 224(6) (2010), 2472–2484.Google Scholar
8.Chouraqui, F., Garside groups and Yang–Baxter equation, Commun. Algebra 38(12) (2010), 4441–4460.Google Scholar
9.Chouraqui, F., Left orders in Garside groups, Int. J. Algebra Comput. 26(7) (2016), 1349–1359.Google Scholar
10.Chouraqui, F. and Godelle, E., Finite quotients of groups of I-type, Adv. Math. 258 (2014), 46–68.Google Scholar
11.Dehornoy, P., Set-theoretic solutions of the Yang–Baxter equation, RC-calculus, and Garside germs, Adv. Math. 282 (2015), 93–127.Google Scholar
12.Dehornoy, P., Dynnikov, I., Rolfsen, D. and Wiest, B., Ordering braids, Mathematical Surveys and Monographs, Volume 148 (American Mathematical Society, Providence, RI, 2008).Google Scholar
13.Deroin, B., Navas, A. and Rivas, C., Groups, orders, and dynamics, preprint (arxiv:1408.5805, 2014).Google Scholar
14.Drinfel'd, V. G., On some unsolved problems in quantum group theory, in Quantum groups (Leningrad, 1990), Lecture Notes in Mathematics, Volume 1510, pp. 1–8 (Springer, Berlin, 1992).Google Scholar
15.Etingof, P., Schedler, T. and Soloviev, A., Set-theoretical solutions to the quantum Yang–Baxter equation, Duke Math. J. 100(2) (1999), 169–209.Google Scholar
16.Fenn, R., Rourke, C. and Sanderson, B., An introduction to species and the rack space, in Topics in knot theory (Erzurum, 1992), NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, Volume 399, pp. 33–55 (Kluwer Academic Publishers, Dordrecht, 1993).Google Scholar
17.Gateva-Ivanova, T. and Cameron, P., Multipermutation solutions of the Yang–Baxter equation, Commun. Math. Phys. 309(3) (2012), 583–621.Google Scholar
18.Gateva-Ivanova, T. and Majid, S., Matched pairs approach to set theoretic solutions of the Yang–Baxter equation, J. Algebra 319(4) (2008), 1462–1529.Google Scholar
19.Gateva-Ivanova, T. and Van den Bergh, M., Semigroups of I-type, J. Algebra 206(1) (1998), 97–112.Google Scholar
20.Graña, M., Heckenberger, I. and Vendramin, L., Nichols algebras of group type with many quadratic relations, Adv. Math. 227(5) (2011), 1956–1989.Google Scholar
21.Guarnieri, L. and Vendramin, L., Skew braces and the Yang–Baxter equation, Math. Comput. 86(307) (2017), 2519–2534.Google Scholar
22.Jespers, E. and Okniński, J., Monoids and groups of I-type, Algebr. Represent. Theory 8(5) (2005), 709–729.Google Scholar
23.Jespers, E. and Okniński, J., Noetherian semigroup algebras, Algebras and Applications, Volume 7 (Springer, Dordrecht, 2007).Google Scholar
24.Kionke, S. and Raimbault, J., On geometric aspects of diffuse groups, Doc. Math. 21 (2016), 873–915. With an appendix by Nathan Dunfield.Google Scholar
25.Lebed, V. and Vendramin, L., Homology of left non-degenerate set-theoretic solutions to the Yang–Baxter equation, Adv. Math. 304 (2017), 1219–1261.Google Scholar
26.Linnell, P. and Witte Morris, D., Amenable groups with a locally invariant order are locally indicable, Groups Geom. Dyn. 8(2) (2014), 467–478.Google Scholar
27.Lu, J.-H., Yan, M. and Zhu, Y.-C., On the set-theoretical Yang–Baxter equation, Duke Math. J. 104(1) (2000), 1–18.Google Scholar
28.Mal'cev, A. I., On isomorphic matrix representations of infinite groups of matrices, Mat. Sb. 8(1940) (2000), 405–422 (in Russian); Amer. Math. Soc. Transl. (2) 45 (1965), 1–18.Google Scholar
29.Nelson, S. and Vo, J., Matrices and finite biquandles, Homology Homotopy Appl. 8(2) (2006), 51–73.Google Scholar
30.Rotman, J. J., An introduction to the theory of groups, Graduate Texts in Mathematics, Volume 148, 4th edn (Springer-Verlag, New York, 1995).Google Scholar
31.Rump, W., Generalized radical rings, unknotted biquandles, and quantum groups, Colloq. Math. 109(1) (2007), 85–100.Google Scholar
32.Short, H. and Wiest, B., Orderings of mapping class groups after Thurston, Enseign. Math. (2) 46(3-4) (2000), 279–312.Google Scholar
33.Smoktunowicz, A. and Vendramin, L., On skew braces (with an appendix by N. Byott and L. Vendramin), J. Comb. Algebra 2(1) (2018), 47–86.Google Scholar
34.Soloviev, A., Non-unitary set-theoretical solutions to the quantum Yang–Baxter equation, Math. Res. Lett. 7(5–6) (2000), 577–596.Google Scholar
35.Szymik, M., Permutations, power operations, and the center of the category of racks, Commun. Algebra 46(1) (2018), 230–240.Google Scholar
36.Vendramin, L., Extensions of set-theoretic solutions of the Yang–Baxter equation and a conjecture of Gateva-Ivanova, J. Pure Appl. Algebra 220(5) (2016), 2064–2076.Google Scholar