Article contents
On some definite integrals involving Legendre functions
Published online by Cambridge University Press: 20 January 2009
Extract
A few definite integrals involving more than two Legendre functions in the integrand have been considered by Ferrers, Adams, Dougall, Nicholson and Bailey. We take for example the following integrals.
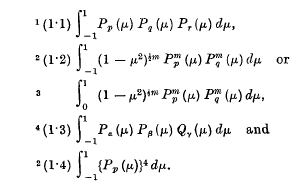
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1934
References
page 41 note 1 Hobson, Spherical and Ellipsoidal Harmonics, p. 87. The references to Ferrers and Adams, who considered this integral, are given there.Google Scholar
page 41 note 2 Bailey, W. N. “On the product of two Legendre functions,” Proc. Camb. Phil.Soc. 29 (1933), 173, results (4·1) and (4·2).CrossRefGoogle Scholar
page 41 note 3 Dougall, J., Proc. Edin. Math. Soc. 37 (1919), 33–47, formula (3).CrossRefGoogle Scholar
page 41 note 4 Nicholson, Phil. Mag. (6) 43 (1922), 783.Google Scholar
page 41 note 5 Phil. Mag. (6), 43 (1922), 1–29,“Zonal Harmonics of the second kind.”CrossRefGoogle Scholar
page 42 note 1 L.c., formula (5·4).
page 42 note 2 I have to thank a referee for suggesting this notation and other modifications in this paper.
page 42 note 3 Prasad, Ganesh, “On non-orthogonal systems of Legendre's functions,” Proc. Benares Math. Soc., 12 (1930), 33–42.Google Scholar
page 42 note 4 Shabde, “On some series and integrals involving Legendre functions,” Bull. Calcutta Math. Soc., 25 (1933), 29.Google Scholar
page 43 note 1 Dhar, and Shabde, , “On the non-orthogonality of Legendre's functions,” Bull. Calcutta Math. Soc., 24 (1932), 185.Google Scholar
page 44 note 1 Prasad, Ganesh, l.c., p. 40.Google Scholar
page 44 note 2 Bailey, W. N., l.c., formula (3·3).Google Scholar
page 45 note 1 Sirkar, H. K., Proc. Edtn. Math. Soc., 2, 1 (1927–1929), 244, “On the evaluation of ![]() and
and ![]() .”Google Scholar
.”Google Scholar
page 46 note 1 L.c., p. 38.
page 46 note 2 Phil. Mag. (6), 43 (1922), 1–29.CrossRefGoogle Scholar
- 1
- Cited by


