No CrossRef data available.
Article contents
On Series for calculating Euler's Constant, and the Constant in Stirling's Theorem
Published online by Cambridge University Press: 20 January 2009
Extract
Let γn denote the value of
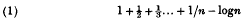
where n is a definite integer; and let γ denote the limit of
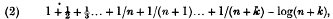
when the integer k is indefinitely increased. It is known that the expansion of γn – γ in ascending powers of 1/n is
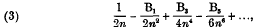
where B1, B3, B5… are the numbers of Bernoulli. The series (3) is, however, divergent, as B2r+1 not only increases indefinitely with r, but bears† an infinite ratio to B2r–1 in this case. It is proposed to find by elementary methods the expansion of γn – γ up to the term in nr and to estimate the error (of order l/nr+1) made in omitting further terms of series (3). I shall take the case of r = 9, but the process is quite general.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1909
References
page 48 note * Boole, Finite Diff. Ch. V. (Euler-Maclaurin Formula); Todhunter, Integral Calc. Ch. XII
page 48 note † Chrystal, Algebra, Ch. XXX.
page 50 note * Chrystal, Algebra Ch. XXXI.
page 50 note † The coefficients on the right side may be thus calculated: write down those of the right side of (6) ; multiply the first by 22 and subtract from the second; multiply the result by 32 and subtract from the third; and so on. Thus from 1, – 1, 4, –36, 576 we obtain successively 1, –5, 49, –820, 21076.
page 51 note * The coefficients can again be calculated by a simple rule : write down those of the first equality – 1, ![]() multiply the first by
multiply the first by ![]() and subtract from the second; multiply the result by
and subtract from the second; multiply the result by ![]() and subtract from the third; and so on, Thus we get 1,
and subtract from the third; and so on, Thus we get 1, ![]()
page 51 note * As a matter of fact the series up to n 8 gives in this case a value correct to 18 places; we are, however, able as shown above to prove that the remaining terms of the series can at most affect the 18th place. For the use of the convergent portion only of series (3), see Boole, Finite Diff. Ch. VIII., and Bromwich, Infinite Series Ch. XI. The latter has proved the approximation to thiee terms of the series by definite integration in Mess. of Math., Vol. XXXVI., 6.Google Scholar
page 57 note * SeeEncy. Brit. ed. IX., 8.v. Infinitesimal Calculus (B. Williamson); also Mess. of Math., Vol. I. (G. W. L. Glaisher).Google Scholar
page 58 note * Chrystal, Algebra, Ch. XXX
page 59 note * Ency. Brit., loc. cit.


