Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-30T15:08:59.605Z Has data issue: false hasContentIssue false
  • English
  • Français

On semigroup algebras and semisimple semilattice sums of rings

Published online by Cambridge University Press:  20 January 2009

Mark L. Teply
Mark L. Teply
Affiliation:
University of FloridaGainesville, Florida 32611, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let P be a semilattice. In (5), a ring T is called a supplementary semilattice sum of subringsTα (α∈P) if the following conditions hold: 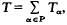TαTβ⊆Tαβ for all α,β∈P, and 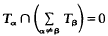for each α∈P. Thus, as an abelian group, T is a direct sum of the additive subgroups Tα (α∈P), and the multiplicative structure of T is strongly influenced by the semilattice P. Properties of these rings have been studied extensively in (2), (3), (5), and (6).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 24 , Issue 2 , June 1981 , pp. 87 - 90
Copyright
Copyright © Edinburgh Mathematical Society 1981

References

REFERENCES

(1)Clifford, A. H. and Preston, G. B., Algebraic Theory of Semigroups, Vol. I. (Math. Surveys of the Amer. Math. Soc., Providence, R. I., 1961).CrossRefGoogle Scholar
(2)Gardner, B. J., Radicals of supplementary semilattice sums of associative rings, Pacific J. Math. 58 (1975), 387–392.CrossRefGoogle Scholar
(3)Janeski, J. and Weissglass, J., Regularity of semilattice sums of rings, Proc. Amer. Math. Soc. 39 (1973), 479–482.CrossRefGoogle Scholar
(4)Petrich, M., Introduction to Semigroups (C. Merrill, Columbus, Ohio, 1973).Google Scholar
(5)Teply, M. L., Turman, E. G., and Quesada, A., On Semisimple semigroup Rings, Proc. Amer. Math. Soc. 79 (1980), 157–163.CrossRefGoogle Scholar
(6)Weissglass, J., Semigroup Rings and Semilattice Sums of Rings, Proc. Amer. Math. Soc. 39 (1973), 471–478.CrossRefGoogle Scholar