Article contents
On ideally finite Lie algebras which are lower semi-modular
Published online by Cambridge University Press: 20 January 2009
Extract
The purpose of this paper is twofold: first to correct the statement of Theorem 1 in [4], and secondly to consider related problems in the class of ideally finite Lie algebras.
Throughout, L will denote a Lie algebra over a field K, F(L) will be its Frattini subalgebra and φ(L) its Frattini ideal. We will denote by 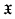 the class of Lie algebras all of whose maximal subalgebras have codimension 1 in L. The Lie algebra with basis {u–1, u0, u1} and multiplication u–1u0 = u–1, u–1u1 = u0, u0u1 = u1 will be labelled L1(0).
the class of Lie algebras all of whose maximal subalgebras have codimension 1 in L. The Lie algebra with basis {u–1, u0, u1} and multiplication u–1u0 = u–1, u–1u1 = u0, u0u1 = u1 will be labelled L1(0).
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 28 , Issue 1 , February 1985 , pp. 9 - 11
- Copyright
- Copyright © Edinburgh Mathematical Society 1985
References
REFERENCES
- 1
- Cited by


