Article contents
On Generating Functions
Published online by Cambridge University Press: 20 January 2009
Extract
It is well known that the polynomial in x,
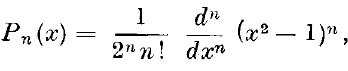
has the following properties:—
(A) it is the coefficient of tn in the expansion of (1–2xt+t2)–½;
(B) it satisfies the three-term recurrence relation
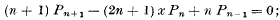
(C) it is the solution of the second order differential equation
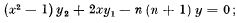
(D) the sequence Pn(x) is orthogonal for the interval (— 1, 1),
i.e. when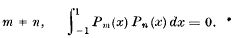
Several other familiar polynomials, e.g., those of Laguerre Hermite, Tschebyscheff, have properties similar to some or all of the above. The aim of the present paper is to examine whether, given a sequence of functions (polynomials or not) which has one of these properties, the others follow from it : in other words we propose to examine the inter-relation of the four properties. Actually we relate each property to the generating function.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1930
References
page 82 note 1 Laurent, , Journal de Math. (3) 1 (1875), 390.Google Scholar
page 82 note 2 The direct verification of the fact that (24) is a solution of (25) is a rather heavy piece of calculation.
- 1
- Cited by


