Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-23T19:02:57.439Z Has data issue: false hasContentIssue false
  • English
  • Français

On functions with derivative of bounded variation: An analogue of Banach's indicatrix theorem

Published online by Cambridge University Press:  20 January 2009

Wolfgang Stadje
Wolfgang Stadje
Affiliation:
Universitat Osnabrock
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A simple, but nice theorem of Banach states that the variation of a continuous function F:[a, b]→ ℝ is given by 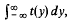where t(y) is defined as the number of x ∈ [a, b[ for which F(x)= y (see, e.g., [1], VIII.5, Th. 3). In this paper we essentially derive a similar representation for the variation of F′ which also yields a criterion for a function to be an integral of a function of bounded variation. The proof given here is quite elementary, though long and somewhat intriciate.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 29 , Issue 1 , February 1986 , pp. 61 - 68
Copyright
Copyright © Edinburgh Mathematical Society 1986

References

REFERENCES

1.Natanson, I. P., Theory of Functions of a Real Variable (Frederick Ungar Publishing Co., New York, 1955).Google Scholar
2.Stadje, W., Bemerkung zu einem Satz von Akcoglu und Krengel, Studia Math. 81 (1985), 307–310.CrossRefGoogle Scholar