No CrossRef data available.
Article contents
On Factors of Numbers of the Form 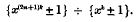
Published online by Cambridge University Press: 20 January 2009
Extract
In this paper the factorization of arithmetical numbers of the form 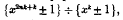 , where x; is a rational number such that kx is a perfect square, is investigated by means of a trigonometrical transformation. The number k will be taken to be prime for the present.
, where x; is a rational number such that kx is a perfect square, is investigated by means of a trigonometrical transformation. The number k will be taken to be prime for the present.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1907
References
page 67 note * See the author's question in the Educational Times for June 1898. Numbers of the form x 4n+2+l have been called Bin-Aurifeuillians by Lt.-Col. Allan Cunningham, R.E., who has dealt with them in a paper “On Aurifeuillians” in the Proceedings of the Lond. Math. Soc., Vol. XXIX. (03 1898).Google Scholar My acknowledgments are due to Lt.-Col. Cunningham for his kindness in allowing me to draw on this paper and on his solutions in the Reprints from the Educ. Tim. for most of my illustrative examples.
page 69 note * See Reprint E. T., Vol. LXX. (Lt.-Col. Cunningham).Google Scholar
page 70 note * By MrBiokmore, C. E. (Lt.-Col. Cunningham's paper, Proc. Land. Math. Soc. XXIX.).Google Scholar
page 71 note * See Proe. Math. Soc. Land. XXIX. (Lt.-Col. Cunningham).Google Scholar
page 72 note * Exoept when n has the value kp + ½ (p – 1), in which case the general prooess fails.
page 74 note * * See Educ. Times for August 1902. Numbers of this form have been called Trin Aurifcuillians by Lt-Col. Cunningham in his paper “On Aurifeuillians” mentioned above. As before I have derived much help from that paper in my examples.
page 75 note * See Reprints E. T., Vol. LXX. (Lt.-Col. Cunningham).Google Scholar
† 1 is algebraically a factor, though it does not count numerically.
page 76 note * Except when q is zero,
page 78 note * See Proc. Land. Math. Soc., XXIX. (Lt.-Col. Cunningham.)Google Scholar
page 80 note * * It should be noticed that in the series f the co-efficients recur reciprocally after the middle term.
page 81 note * Reprintt E.T., Vol. LXX. (Lt.-Col. Cunningham).Google Scholar
page 83 note * The value of ![]() is zero, and the factor corresponding to this function does not occur in the product.
is zero, and the factor corresponding to this function does not occur in the product.
page 84 note * I have no right proof to offer of this statement.


