Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-22T02:08:33.806Z Has data issue: false hasContentIssue false
  • English
  • Français

On discrete generalised triangle groups

Published online by Cambridge University Press:  20 January 2009

M. Hagelberg ,
C. MacLachlan  and
G. Rosenberger
M. Hagelberg
Affiliation:
Institut für Mathematik, Ruhr-Universität Bochum, 4630 Bochum 1, Germany
C. MacLachlan
Affiliation:
Department of Mathematical Sciences, University of Aberdeen, Aberdeen AB9 2RY, Scotland
G. Rosenberger
Affiliation:
Fachbereich Mathematik, Universität Dortmund, 4600 Dortmund 50, Germany
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A generalised triangle group has a presentation of the form

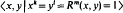
where R is a cyclically reduced word involving both x and y. When R = xy, these classical triangle groups have representations as discrete groups of isometrics of S2, R2, H2 depending on

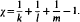
In this paper, for other words R, faithful discrete representations of these groups in Isom +H3 = PSL(2, C) are considered with particular emphasis on the case R = [x, y] and also on the relationship between the Euler characteristic χ and finite covolume representations.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 38 , Issue 3 , October 1995 , pp. 397 - 412
Copyright
Copyright © Edinburgh Mathematical Society 1995

References

REFERENCES

1.Borel, A., Commensurability classes and volumes of hyperbolic 3-manifolds, Ann. Scuola Norm. Sup. Pisa Cl. Sci. 8 (1981), 1–33.Google Scholar
2.Baumslag, G., Morgan, J. and Shalen, P., Generalised triangle groups, Math. Proc. Cambridge Philos. Soc. 102 (1987), 25–31.CrossRefGoogle Scholar
3.Coxeter, H. S. M., The groups determined by the relations S 1=T m = (S -1T -1ST)p=l, Duke Math. J. 2 (1936), 61–73.Google Scholar
4.Conder, M. D. E. and Martin, G., Cusps, triangle groups and hyperbolic 3-folds, J. Australian Math. Soc. 55 (1993), 149–182.Google Scholar
5.Dunbar, W., Geometric orbifolds, Revista Math. 1 (1988), 67–99.Google Scholar
6.Fine, B., The Algebraic Theory of the Bianchi groups (Marcel Dekker 1989).Google Scholar
7.Fine, B., Howie, J. and Rosenberger, G., One-relator quotients and free products of cycles, Proc. Amer. Math. Soc. 102 (1988), 249–254.Google Scholar
8.Fine, B. and Rosenberger, G., A note on generalised triangle groups, Abh. Math. Sent. Univ. Hambur. 56 (1986), 233–244.CrossRefGoogle Scholar
9.Fine, B., Rosenberger, G. and Stille, M., Euler characteristic for one-relator products of cyclics, Comm. Algebra 21(12) (1993), 4353–4359.CrossRefGoogle Scholar
10.Hagelberg, M., Hyperbolic 3-dimensional orbifolds (Proc. NATO Conf. on Knot Theory, Erzurum, Turkey, 1992).Google Scholar
11.Hagelberg, M., Generalised triangle groups and 3-dimensional orbifolds (SFB 343 Bielefeld, Diskrete Strukturen in der Mathematik. Preprint 92–049 (1992)).Google Scholar
12.Helling, H., Mennicke, J. and Vinberg, E., On some general triangle groups and 3-dimensional orbifolds, Trans. Moscow Math. Soc., to appear.Google Scholar
13.Howie, J., Metaftsis, V. and Thomas, R. M., Finite generalised triangle groups, Trans. Amer. Math. Soc, to appear.Google Scholar
14.Limenko, E. Ya K., Discrete groups in three-dimensional Lobachevsky space generated by two rotations. Siberian Math. J. 130 (1989), 123–128.Google Scholar
15.Levin, F. and Rosenberger, G., A class of SQ-universal groups, in Group Theory (Proc. of 1987 Conf. Singapore 1989), 409–415.Google Scholar
16.Maskit, B., Kleinian groups (Grundlehren der mathematischen Wissenschaften 287, Springer 1988).Google Scholar
17.Mednykh, A., Automorphism groups of 3-dimensional hyperbolic manifolds, Soviet Math. Dokl. 32 (1985), 633–636.Google Scholar
18.Maclachlan, C. and Reid, A. W., Commensurability classes of arithmetic Kleinian groups and their Fuchsian subgroups, Math. Proc. Cambridge Philos. Soc. 102 (1987), 251–257.CrossRefGoogle Scholar
19.Neumann, W. and Reid, A. W., Arithmetic of hyperbolic manifolds, in Topology '90 (De Gruyter 1992), 273–310.CrossRefGoogle Scholar
20.Ratcliffe, J., Euler characteristics of 3-manifold groups and discrete subgroups of SL2(C), J. Pure Appl. Alg. 44 (1987), 303–314.CrossRefGoogle Scholar
21.Reid, A. W., Arithmetic Kleinian groups and their Fuchsian subgroups (Thesis, Aberdeen University 1987).Google Scholar
22.Rosenberger, G., Eine Bemerkung zu einer Arbeit von T. Jorgensen, Math. Zt. 165 (1979), 261–265.CrossRefGoogle Scholar
23.Takeuchi, K., A characterisation of arithmetic Fuchsian groups, J. Math. Soc. Japa. 27 (1975), 600–612.Google Scholar
24.Thurston, W., The geometry and topology of three-manifolds (Lecture Notes, Princeton 1980).Google Scholar
25.Vigneras, M. -F., Arithmetique des Algebres de Quaternions [Lecture Notes in Maths, 800, Springer 1980).CrossRefGoogle Scholar