Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-29T01:02:31.206Z Has data issue: false hasContentIssue false
  • English
  • Français

On conjugacy of subalgebras in graph C*-algebras. II

Part of: Selfadjoint operator algebras Algebraic number theory: global fields

Published online by Cambridge University Press:  09 December 2022

Tomohiro Hayashi ,
Jeong Hee Hong  and
Wojciech Szymański
Tomohiro Hayashi
Affiliation:
Nagoya Institute of Technology, Gokiso-cho,Showa-ku, Nagoya, Aichi 466–8555, Japan ([email protected])
Jeong Hee Hong
Affiliation:
Department of Mathematics and Computer Science, The University of Southern Denmark, Campusvej 55, DK–5230 Odense M, Denmark ([email protected]; [email protected])
Wojciech Szymański
Affiliation:
Department of Mathematics and Computer Science, The University of Southern Denmark, Campusvej 55, DK–5230 Odense M, Denmark ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We apply a method inspired by Popa's intertwining-by-bimodules technique to investigate inner conjugacy of MASAs in graph $C^*$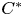-algebras. First, we give a new proof of non-inner conjugacy of the diagonal MASA ${\mathcal {D}}_E$ 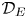to its non-trivial image under a quasi-free automorphism, where $E$ 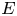is a finite transitive graph. Changing graphs representing the algebras, this result applies to some non quasi-free automorphisms as well. Then, we exhibit a large class of MASAs in the Cuntz algebra ${\mathcal {O}}_n$ 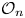that are not inner conjugate to the diagonal ${\mathcal {D}}_n$.

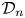Keywords

Graph C*-algebraMASAautomorphism

MSC classification

Primary: 46L05: General theory of $C^*$-algebras 46L40: Automorphisms 11R04: Algebraic numbers; rings of algebraic integers
Secondary: 11R21: Other number fields
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 4 , November 2022 , pp. 1162 - 1182
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avery, J. E., Johansen, R. and Szymański, W., Visualizing automorphisms of graph algebras, Proc. Edinburgh Math. Soc. 61 (2018), 215–249.CrossRefGoogle Scholar
Bates, T. and Pask, D., Flow equivalence of graph algebras, Ergod. Th. Dynam. Sys. 24 (2004), 367–382.CrossRefGoogle Scholar
Bates, T., Pask, D., Raeburn, I. and Szymański, W., The $C^*$-algebras of row-finite graphs, New York J. Math. 6 (2000), 307–324.Google Scholar
Conti, R., Hong, J. H. and Szymański, W., Endomorphisms of graph algebras, J. Funct. Anal. 263 (2012), 2529–2554.CrossRefGoogle Scholar
Conti, R., Hong, J. H. and Szymański, W., On conjugacy of MASAs and the outer automorphism group of the Cuntz algebra, Proc. R. Soc. Edinburgh 145 (2015), 269–279.CrossRefGoogle Scholar
Conti, R. and Pinzari, C., Remarks on the index of endomorphisms of Cuntz algebras, J. Funct. Anal. 142 (1996), 369–405.CrossRefGoogle Scholar
Conti, R. and Szymański, W., Labeled trees and localized automorphisms of the Cuntz algebras, Trans. Amer. Math. Soc. 363 (2011), 5847–5870.CrossRefGoogle Scholar
Cuntz, J., Simple $C^*$-algebras generated by isometries, Comm. Math. Phys. 57 (1977), 173–185.CrossRefGoogle Scholar
Cuntz, J., Automorphisms of certain simple $C^*$-algebras, In Quantum fields-algebras-processes (Bielefield, 1978) (ed. L. Streit), pp. 187–196 (Springer, Vienna, 1980).CrossRefGoogle Scholar
Cuntz, J. and Krieger, W., A class of $C^*$-algebras and topological Markov chains, Invent. Math. 56 (1980), 251–268.CrossRefGoogle Scholar
Donsig, A. P. and Power, S. C., The failure of approximate inner conjugacy for standard diagonals in regular limit algebras, Canad. Math. Bull. 39 (1996), 420–428.CrossRefGoogle Scholar
Goodman, F. M., de la Harpe, P. and Jones, V. F. R., Coxeter graphs and towers of algebras, M. S. R. I. Publ. Vol. 14 (Springer-Verlag, New York, 1989).CrossRefGoogle Scholar
Graham, A., Nonnegative matrices and applicable topics in linear algebra (New York, John Wiley & Sons, 1987).Google Scholar
Hayashi, T., Hong, J. H., Mikkelsen, S. E. and Szymański, W., On conjugacy of subalgebras of graph $C^*$-algebras, In Proceedings of the 37$^{\rm th}$ Workshop on Geometric Methods in Physics (Białowieża, July 2018) (Trends in Mathematics, Birkhäuser, 2019), pp. 163–173.CrossRefGoogle Scholar
Hopenwasser, A., Peters, J. R. and Power, S. C., Subalgebras of graph $C^*$-algebras, New York J. Math. 11 (2005), 351–386.Google Scholar
Houdayer, C. and Isono, Y., Unique prime factorization and bicentralizer problem for a class of type $III$ factors, Adv. Math. 305 (2017), 402–455.CrossRefGoogle Scholar
Houdayer, C. and Vaes, S., Type $III$ factors with unique Cartan decomposition, J. Math. Pures Appl. 100 (2013), 564–590.CrossRefGoogle Scholar
Johansen, R., Sørensen, A. P. W. and Szymański, W., The polynomial endomorphisms of graph algebras, Groups, Geom., Dyn. 14 (2020), 1043–1075.CrossRefGoogle Scholar
Kumjian, A., Pask, D. and Raeburn, I., Cuntz-Krieger algebras of directed graphs, Pacific J. Math. 184 (1998), 161–174.CrossRefGoogle Scholar
Kumjian, A., Pask, D., Raeburn, I. and Renault, J., Graphs, groupoids, and Cuntz-Krieger algebras, J. Funct. Anal. 144 (1997), 505–541.CrossRefGoogle Scholar
Packer, J. A., Point spectrum of ergodic abelian group actions and the corresponding group-measure factors, Pacific J. Math. 119 (1985), 381–d405.CrossRefGoogle Scholar
Popa, S., Strong rigidity of type $II_1$ factors arising from malleable actions of $w$-rigid groups I, Invent. Math. 165 (2006), 369–408.CrossRefGoogle Scholar
Speelman, A. and Vaes, S., A class of $II_1$ factors with many non conjugate Cartan subalgebras, Adv. Math. 231 (2012), 2224–2251.CrossRefGoogle Scholar
Zacharias, J., Quasi-free automorphisms of Cuntz-Krieger-Pimsner algebras, In $C^*$-algebras (Münster, 1999), pp. 262–272 (Springer, Berlin, 2000).CrossRefGoogle Scholar