On completely singular von Neumann subalgebras

Junsheng Fang

doi:10.1017/S0013091507000958

On completely singular von Neumann subalgebras

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press: 23 September 2009

Junsheng Fang

Show author details

Junsheng Fang: Affiliation:
Department of Mathematics, University of New Hampshire, Durham, NH 03824, USA; Email: ([email protected])

Article contents

Abstract

Rights & Permissions

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ℳ be a von Neumann algebra acting on a Hilbert space and let 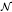be a von Neumann subalgebra of ℳ. If 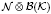is singular in 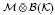for every Hilbert space 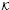, 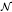is said to be completely singular in ℳ. We prove that if 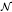is a singular abelian von Neumann subalgebra or if 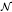is a singular subfactor of a type-II1 factor ℳ, then 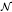is completely singular in ℳ. is separable, we prove that 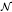is completely singular in ℳ if and only if, for every θ∈Aut(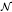′) such that θ(X)=X for all X ∈ ℳ′, θ(Y)=Y for all Y∈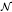′. As the first application, we prove that if ℳ is separable (with separable predual) and 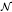is completely singular in ℳ, then 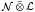is completely singular in 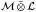for every separable von Neumann algebra 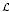. As the second application, we prove that if 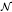1 is a singular subfactor of a type-II1 factor ℳ1 and 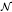2 is a completely singular von Neumann subalgebra of ℳ2, then 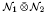is completely singular in .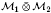