Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T08:36:25.149Z Has data issue: false hasContentIssue false
  • English
  • Français

On birationally trivial families and adjoint quadrics

Part of: Cycles and subschemes Families, fibrations Birational geometry Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  04 July 2022

Luca Cesarano ,
Luca Rizzi Open the ORCID record for Luca Rizzi [Opens in a new window]  and
Francesco Zucconi Open the ORCID record for Francesco Zucconi [Opens in a new window]
Luca Cesarano
Affiliation:
Mathematisches Institut, Universität Bayreuth, Universitätsstraße 30, 95447 Bayreuth, Germany ([email protected])
Luca Rizzi
Affiliation:
IBS Center for Complex Geometry, 55 EXPO-ro, Yuseong-gu, 34126 Daejeon, South Korea ([email protected])
Francesco Zucconi
Affiliation:
DMIF, Università di Udine, Via delle Scienze 206, 33100 Udine, Italy ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $\pi \colon \mathcal {X}\to B$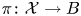 be a family whose general fibre $X_b$ 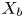is a $(d_1,\,\ldots,\,d_a)$-polarization on a general abelian variety, where $1\leq d_i\leq 2$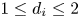, $i=1,\,\ldots,\,a$ 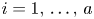and $a\geq 4$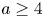. We show that the fibres are in the same birational class if all the $(m,\,0)$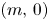-forms on $X_b$ 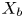are liftable to $(m,\,0)$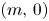-forms on $\mathcal {X}$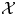, where $m=1$ and $m=a-1$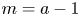. Actually, we show a general criteria to establish whether the fibres of certain families belong to the same birational class.

Keywords

extension class of a vector bundleholomorphic formsAlbanese varietyfamilies of varietiesinfinitesimal invariant

MSC classification

Primary: 14J10: Families, moduli, classification 14C34: Torelli problem 14D07: Variation of Hodge structures
Secondary: 14E99: None of the above, but in this section 14J40: $n$-folds ($n>4$)
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 3 , August 2022 , pp. 587 - 617
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arbarello, E. and Cornalba, M., Su una congettura di Petri, Comment. Math. Helv. 56 (1981), 1–38.CrossRefGoogle Scholar
Barja, M.Á, González-Alonso, V. and Naranjo, J. C., Xiao's conjecture for general fibred surfaces, J. Reine Angew. Math. 739 (2018), 297–308.CrossRefGoogle Scholar
Birkenhake, C. and Lange, H., Complex abelian varieties, Grundlehren der mathematischen Wissenschaften 302, A Series of Comprehensive Studies in Mathematics (Springer-Verlag, Berlin Heidelberg, 1992).Google Scholar
Bloss, P., The infinitesimal Torelli theorem for hypersurfaces in abelian varieties, Preprint, available at https://arxiv.org/abs/1911.08311Google Scholar
Catanese, F., Monodromy and normal forms (eds W. König and J. Sprekels), Karl Weierstraß (1815-1897) (Springer Spektrum, Wiesbaden, 2016).CrossRefGoogle Scholar
Cesarano, L., Canonical surfaces and hypersurfaces in abelian varieties. Preprint, available at https://arxiv.org/abs/1808.05302 (2018)Google Scholar
Collino, A. and Pirola, G. P., The Griffiths infinitesimal invariant for a curve in its Jacobian, Duke Math. J. 78(1) (1995), 59–88.CrossRefGoogle Scholar
Fakhruddin, N., Algebraic cycles on generic abelian varieties, Comp. Math. 100 (1996), 101–119.Google Scholar
González-Alonso, V., Hodge numbers of irregular varieties and fibrations, Ph.D. Thesis (2013).Google Scholar
González-Alonso, V., A generalization of the Castelnuovo-de Franchis inequality, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 15 (2016), 173–182.Google Scholar
González-Alonso, V., On deformations of curves supported on rigid divisors, Ann. Mat. Pura Appl. (4) 195(1) (2016), 111–132.CrossRefGoogle Scholar
González-Alonso, V., Stoppino, L. and Torelli, S., On the rank of the flat unitary summand of the Hodge bundle, Trans. Amer. Math. Soc. 372 (2019), 8663–8677.CrossRefGoogle Scholar
Griffiths, P., Periods of integrals on algebraic manifolds I, II, Amer. J. Math. 90 (1968), 568–626805–865CrossRefGoogle Scholar
Griffiths, P., Periods of integrals on algebraic manifolds III. Some global differential-geometric properties of the period mapping, Inst. Hautes Études Sci. Publ. Math. No. 38 (1970), 125–180.CrossRefGoogle Scholar
Kollár, J., Families of varieties of general type, available at https://web.math.princeton.edu/kollar/book/modbook20170720.pdf (2017)Google Scholar
Möller, M., Maximally irregularly fibred surfaces of general type, Manuscripta Math. 116(1) (2005), 71–92.CrossRefGoogle Scholar
Nori, M. V., Algebraic cycles and Hodge theoretic connectivity, Inv. Math. 111 (1993), 349–373.CrossRefGoogle Scholar
Oort, F. and Steenbrink, J., The local Torelli problem for algebraic curves, Journées de Géométrie Algébrique d'Angers, Juillet 1979/Algebraic Geometry, Angers, 1979, pp. 157–204, Sijthoff and Noordhoff, Alphen aan den Rijn–Germantown, Md., (1980)Google Scholar
Peters, C., Some remarks about Reider's article “Infinitesimal Torelli Theorem for certain irregular surfaces of general type”, Math. Ann. 281 (1988), 315–324.CrossRefGoogle Scholar
Pirola, G. P., On a conjecture of Xiao, J. Reine Angew. Math. 431 (1992), 75–89.Google Scholar
Pirola, G. P., On the Abel–Jacobi image of cycles for a generic abelian fourfold, Bollettino U.M.I. 8-A(7) (1994), 83–93.Google Scholar
Pirola, G. P. and Torelli, S., Massey products and Fujita decompositions on fibrations of curves, Collect. Math. 71 (2020), 39–61.CrossRefGoogle Scholar
Pirola, G. P. and Zucconi, F., Variations of the Albanese morphisms, J. Algebraic Geom. 12(3) (2003), 535–572.CrossRefGoogle Scholar
Reider, I., On the Infinitesimal Torelli Theorem for certain irregular surfaces of general type, Math. Ann. 280 (1988), 285–302.CrossRefGoogle Scholar
Rizzi, L., On Massey products and rational homogeneous varieties, https://arxiv.org/abs/2012.06375, (2020)Google Scholar
Rizzi, L. and Zucconi, F., Generalized adjoint forms on algebraic varieties, Ann. Mat. Pura Appl. 196 (2017), 819–836.CrossRefGoogle Scholar
Rizzi, L. and Zucconi, F., On Green's proof of infinitesimal Torelli theorem for hypersurfaces, Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. 4 (2018), 689–709.CrossRefGoogle Scholar
Rizzi, L. and Zucconi, F., Differential forms and quadrics of the canonical image, Ann. Mat. Pura Appl. 199(6) (2020), 2341–2356.CrossRefGoogle Scholar
Rizzi, L. and Zucconi, F., Fujita decomposition and Massey product for fibered varieties, Nagoya Math. J. (2021), 1–29. https://doi.org/10.1017/nmj.2021.15Google Scholar
Torelli, S., Fujita decompositions and infinitesimal invariants on fibred surfaces, Ph.D. Thesis (2018).Google Scholar
Voisin, C., Une Remarque Sur l'Invariant Infinitésimal Des Fonctions Normales, C. R. Acad. Sci. Paris Ser. I. Math. 307 (1988), 157–160.Google Scholar
Xiao, G., Fibered algebraic surfaces with low slope, Math. Ann. 276 (1987), 449–466.Google Scholar