Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T07:20:57.606Z Has data issue: false hasContentIssue false
  • English
  • Français

On bar lengths in partitions

Part of: Representation theory of groups

Published online by Cambridge University Press:  21 March 2013

Jean-Baptiste Gramain  and
Jørn B. Olsson
Jean-Baptiste Gramain
Affiliation:
Institute of Mathematics, University of Aberdeen, Fraser Noble Building, Aberdeen AB24 3UE, UK ([email protected])
Jørn B. Olsson
Affiliation:
Department of Mathematical Sciences, University of Copenhagen, Universitetsparken 5, 2100 Copenhagen Ø, Denmark ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We present, given an odd integer d, a decomposition of the multiset of bar lengths of a bar partition λ as the union of two multisets, one consisting of the bar lengths in its d-core partition cd(λ) and the other consisting of modified bar lengths in its d-quotient partition. In particular, we obtain that the multiset of bar lengths in cd(λ) is a sub-multiset of the multiset of bar lengths in λ. Also, we obtain a relative bar formula for the degrees of spin characters of the Schur extensions of 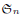. The proof involves a recent similar result for partitions, proved by Bessenrodt and the authors.

Keywords

partitionsbar partitionsbar lengthssymmetric groupcovering groups

MSC classification

Secondary: 20C30: Representations of finite symmetric groups 20C15: Ordinary representations and characters 20C20: Modular representations and characters
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 56 , Issue 2 , June 2013 , pp. 535 - 550
Copyright
Copyright © Edinburgh Mathematical Society 2013

References

1.Bessenrodt, C., Gramain, J.-B. and Olsson, J. B., Generalized hook lengths in symbols and partitions, J. Algebraic Combin. 36 (2012), 309–332.CrossRefGoogle Scholar
2.James, G. and Kerber, A., The representation theory of the symmetric group, Encyclopedia of Mathematics and Its Applications, Volume 16 (Addison-Wesley, Reading, MA, 1981).Google Scholar
3.Macdonald, I. G., Symmetric functions and Hall polynomials, Oxford Mathematical Monographs, Volume 16 (The Clarendon Press, New York, 1979).Google Scholar
4.Morris, A. O., The spin representation of the symmetric group, Can. J. Math. 17 (1965), 543–549.CrossRefGoogle Scholar
5.Morris, A. O. and Yaseen, A. K., Some combinatorial results involving shifted Young diagrams, Math. Proc. Camb. Phil. Soc. 99 (1986), 23–31.CrossRefGoogle Scholar
6.Olsson, J. B., Combinatorics and representations of finite groups, Vorlesungen aus dem Fachbereich Mathematik der Universität Essen, Heft 20 (1993; available at www.math.ku.dk/~olsson/).Google Scholar
7.Schur, I., Über die Darstellung der symmetrischen und der alternierenden Gruppe durch gebrochene lineare Substitutionen, J. Reine Angew. Math. 139 (1911), 155–250Google ScholarGoogle Scholar