Article contents
On an Integral due to Ramanujan, and some ideas suggested by it
Published online by Cambridge University Press: 20 January 2009
Extract
By applying Fourier's Integral Theorem to a well-known formula, due to Cauchy, expressed in the form
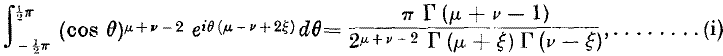
where R (μ + v) > 1, Ramanujan has shown that
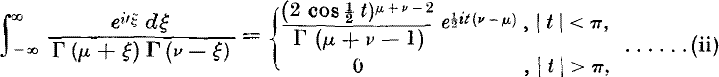
where t is any real number.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1930
References
page 26 note 1 Quart. Journ. of Maths., 48 (1920), 294–310.Google Scholar
page 27 note 1 Whittaker, and Watson, , Modern Analysis, 2nd Ed., p. 309.Google Scholar
page 27 note 2 Proc. Lond. Math. Soc., Ser. 2, 26 (1925), 76.Google Scholar
page 28 note 1 This is a special case of an integral due to Gegenbauer. For references, see Watson, , Bessel Functions, p. 50.Google Scholar
page 29 note 1 Math. Ann., 16 (1880), 39.Google Scholar
page 30 note 1 Gray, , Mathews, , AND MacRobert, , Bessel Functions, p, 66 (11)Google Scholar
- 1
- Cited by


