No CrossRef data available.
Article contents
On a System of Equations
Published online by Cambridge University Press: 20 January 2009
Extract
I propose to prove the following theorem.
With n > 2, the (n + 2) equations derived from the matrix

where
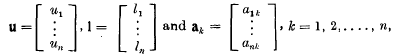
by equating to zero all (n + 1)-rowed determinants from the matrix ‖Δ‖ are equivalent to only two, one of which is linear in li (i = 1, 2, …, n) and the other is homogeneous and quadratic in a certain n – 1 of li (i = 1, 2, …, n); the elements of the matrix are real; 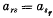 (r, s = 1, 2, …, n) and d is arbitrary.
(r, s = 1, 2, …, n) and d is arbitrary.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 8 , Issue 3 , December 1949 , pp. 101 - 105
- Copyright
- Copyright © Edinburgh Mathematical Society 1949
References
1 See Bôcher, , Introduction to Higher Algebra (1938), p. 58.Google Scholar


