No CrossRef data available.
Published online by Cambridge University Press: 20 January 2009
At a recent meeting of the Royal Society of Edinburgh, Professor Tait proposed and solved the following problem:—
To calculate the number of Partitions of any number that can be made by taking any number from 2 up to another given number.
Let us denote by 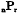 the number of partitions of r obtained by taking any of the numbers 2, 3, 4,……(n − 1), n. In the particular case n = 7, r = 10, the actual partitions are 3 + 7, 4 + 6, 5 + 5; 2 + 2 + 6, 2 + 3 + 5, 2 + 4 + 4, 3 + 3 + 4; 2 + 2 + 2 + 4, 2 + 2 + 3 + 3; 2 + 2 + 2 + 2 + 2; ten in all. Hence
the number of partitions of r obtained by taking any of the numbers 2, 3, 4,……(n − 1), n. In the particular case n = 7, r = 10, the actual partitions are 3 + 7, 4 + 6, 5 + 5; 2 + 2 + 6, 2 + 3 + 5, 2 + 4 + 4, 3 + 3 + 4; 2 + 2 + 2 + 4, 2 + 2 + 3 + 3; 2 + 2 + 2 + 2 + 2; ten in all. Hence 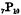 =10.
=10.