Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-27T20:34:14.993Z Has data issue: false hasContentIssue false
  • English
  • Français

On a generalisation of a result of Ramanujan connected with the exponential series

Published online by Cambridge University Press:  20 January 2009

R. B. Paris
R. B. Paris
Affiliation:
Association Euratom—Cea, Centre d'Etudes Nucleaires, 92260 Fontenay-aux-Roses, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

One of the many interesting problems discussed by Ramanujan is an approximation related to the exponential series for en, when n assumes large positive integer values. If the number θn is defined by

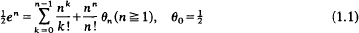
Ramanujan (9) showed that when n is large, θn possesses the asymptotic expansion

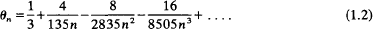
The first demonstrations that θn lies between ½ and 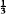and that θn decreases monotoni-cally to the value 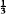as n increases, were given by Szegö (12) and Watson (13). Analogous results were shown to exist for the function e−n, for positive integer values of n, by Copson (4). If φn is defined by

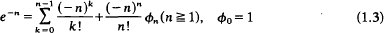
then πn lies between 1 and ½ and tends monotonically to the value ½ as n increases, with the asymptotic expansion

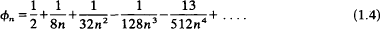
A generalisation of these results was considered by Buckholtz (2) who defined, in a slightly different notation, for complex z and positive integer n, the function φn(z) by

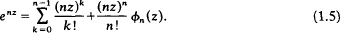
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 24 , Issue 3 , October 1981 , pp. 179 - 195
Copyright
Copyright © Edinburgh Mathematical Society 1981

References

REFERENCES

(1)Abramowitz, M. and Stegun, I. (Eds.), Handbook of Mathematical Functions (Dover, New York; 1965).Google Scholar
(2)Buckholtz, J. D., Concerning an approximation of Copson, Proc. Amer. Math. Soc. 14 (1963), 564–568.CrossRefGoogle Scholar
(3)Carlitz, L., The coefficients in an asymptotic expansion, Proc. Amer. Math. Soc. 16 (1965), 248–252.CrossRefGoogle Scholar
(4)Copson, E. T., An approximation connected with e−x, Proc. Edinburgh Math. Soc. (2), 3 (1932), 201–206.CrossRefGoogle Scholar
(5)Erdelyi, A., Asymptotic Expansions (Dover, New York; 1965).Google Scholar
(6)Jeffreys, H. and Jeffreys, B. S., Methods of Mathematical Physics (Cambridge Univ. Press, 1972).Google Scholar
(7)Knuth, D. E., Fundamental Algorithms (Series in Computer Science and Information Processing, Addison-Wesley, 1973).Google Scholar
(8)Olver, F. W. J., Asymptotics and Special Functions (Academic Press, 1974).Google Scholar
(9)Ramanujan, S., J. Ind. Math. Soc. 3 (1911), 128; J. Ind. Math. Soc. 4 (1911), 151–152; Collected Papers (Chelsea, New York; 1962), 323–324.Google Scholar
(10)Slater, L. J., Generalised Hypergeometric Functions (Cambridge Univ. Press, 1966).Google Scholar
(11)Stokes, G. G., Note on the determination of arbitrary constants which appear as multipliers of semi-convergent series, Proc. Camb. Phil. Soc. 6 (1889), 362–366.Google Scholar
(12)Szegö, G., Uber einige von S. Ramanujan gestellte Aufgaben, J. London Math. Soc. 3 (1928), 225–232.CrossRefGoogle Scholar
(13)Watson, G. N., Theorems stated by Ramanujan: approximations connected with e x, Proc. London Math. Soc. 29 (1928), 293–308.Google Scholar
(14)Watson, G. N., Theory of Bessel Functions (Cambridge Univ. Press, 1944).Google Scholar
(15)Wong, R., On uniform asymptotic expansion of definite integrals, J. Approx. Theory 7 (1973), 76–86.CrossRefGoogle Scholar