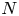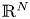Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Candela, Anna Maria
Perera, Kanishka
and
Sportelli, Caterina
2023.
On a class of supercritical N-Laplacian problems.
Nonlinear Analysis: Real World Applications,
Vol. 71,
Issue. ,
p.
103817.