Article contents
A note on the Gaussian cardinal-interpolation operator
Published online by Cambridge University Press: 20 January 2009
Abstract
Suppose λ is a positive number, and let 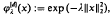 , x∈Rd, denote the d-dimensional Gaussian. Basic theory of cardinal interpolation asserts the existence of a unique function
, x∈Rd, denote the d-dimensional Gaussian. Basic theory of cardinal interpolation asserts the existence of a unique function 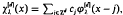 , x∈Rd, satisfying the interpolatory conditions
, x∈Rd, satisfying the interpolatory conditions 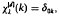 , k∈Zd, and decaying exponentially for large argument. In particular, the Gaussian cardinal-interpolation operator
, k∈Zd, and decaying exponentially for large argument. In particular, the Gaussian cardinal-interpolation operator 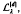 , given by
, given by 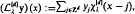 , x∈Rd,
, x∈Rd, 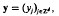 , is a well-defīned linear map from ℓ2(Zd) into L2(Rd). It is shown here that its associated operator-norm is
, is a well-defīned linear map from ℓ2(Zd) into L2(Rd). It is shown here that its associated operator-norm is 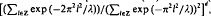 , implying, in particular, that
, implying, in particular, that 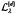 is contractive. Some sidelights are also presented.
is contractive. Some sidelights are also presented.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 40 , Issue 1 , February 1997 , pp. 137 - 149
- Copyright
- Copyright © Edinburgh Mathematical Society 1997
References
REFERENCES
- 8
- Cited by


