Note on The Envelope-Investigation

Extract

Obscurity in the direct discussion of The Envelope, as given in works on Differential Equations, has led writers on The Calculus to define the envelope of a family by a property which all know that it shares with any locus of multiple-points belonging to the family. The following presentation is an attempt by use of systematic notation to make clear the details of the direct process:—

Starting from the definition that

A curve is an envelope of a given family, if at each of its points it touches a member of the family:

let us suppose that a family is specified by the equation

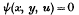
in which ψ is a continuous function of the three variables x, y, u; continuous variation of u corresponds to continuous motion and deformation of a variable curve in the xy-plane, which takes in succession the curves of the family as positions.