Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1969.
The Special Functions and Their Approximations.
Vol. 53,
Issue. ,
p.
330.
1969.
The Special Functions and their Approximations.
Vol. 53,
Issue. ,
p.
453.
Raff, Morton S.
1970.
On Calculating the Gamma Function of Non-Integral Arguments.
The American Statistician,
Vol. 24,
Issue. 2,
p.
22.
Fields, Jerry L.
1973.
Uniform Asymptotic Expansions of Certain Classes of Meijer G-Functions for a Large Parameter.
SIAM Journal on Mathematical Analysis,
Vol. 4,
Issue. 3,
p.
482.
1975.
Mathematical Functions and their Approximations.
p.
517.
Fields, Jerry L.
1983.
Uniform Asymptotic Expansions of a Class of Meijer G-Functions for a Large Parameter.
SIAM Journal on Mathematical Analysis,
Vol. 14,
Issue. 6,
p.
1204.
Frenzen, C. L.
1987.
Error Bounds for Asymptotic Expansions of the Ratio of Two Gamma Functions.
SIAM Journal on Mathematical Analysis,
Vol. 18,
Issue. 3,
p.
890.
Gatteschi, Luigi
1988.
Numerical Integration III.
Vol. 85,
Issue. ,
p.
49.
1989.
Asymptotic Approximations of Integrals.
p.
517.
Frenzen, C. L.
1992.
Error Bounds for the Asymptotic Expansion of the Ratio of Two Gamma Functions with Complex Argument.
SIAM Journal on Mathematical Analysis,
Vol. 23,
Issue. 2,
p.
505.
Chu, David P.T.
1993.
Random r‐content of an r‐simplex from beta‐type‐2 random points.
Canadian Journal of Statistics,
Vol. 21,
Issue. 3,
p.
285.
1996.
Special Functions.
p.
349.
Doman, B.
1996.
An asymptotic expansion for the incomplete beta function.
Mathematics of Computation,
Vol. 65,
Issue. 215,
p.
1283.
Abad, Julio
and
Sesma, Javier
2005.
Two new asymptotic expansions of the ratio of two gamma functions.
Journal of Computational and Applied Mathematics,
Vol. 173,
Issue. 2,
p.
359.
GABETTA, ESTER
and
REGAZZINI, EUGENIO
2010.
ABOUT THE GENE FAMILIES SIZE DISTRIBUTION IN A RECENT MODEL OF GENOME EVOLUTION.
Mathematical Models and Methods in Applied Sciences,
Vol. 20,
Issue. 06,
p.
1005.
Burić, Tomislav
and
Elezović, Neven
2011.
Bernoulli polynomials and asymptotic expansions of the quotient of gamma functions.
Journal of Computational and Applied Mathematics,
Vol. 235,
Issue. 11,
p.
3315.
Qi, Feng
and
Luo, Qiu-Ming
2013.
Bounds for the ratio of two gamma functions: from Wendel’s asymptotic relation to Elezović-Giordano-Pečarić’s theorem.
Journal of Inequalities and Applications,
Vol. 2013,
Issue. 1,
Coelho, Carlos A.
Marques, Filipe J.
and
Oliveira, Sandra
2016.
Near-Exact Distributions for Likelihood Ratio Statistics Used in the Simultaneous Test of Conditions on Mean Vectors and Patterns of Covariance Matrices.
Mathematical Problems in Engineering,
Vol. 2016,
Issue. ,
p.
1.
Sleight, Charlotte
and
Taronna, Massimo
2018.
Anomalous dimensions from crossing kernels.
Journal of High Energy Physics,
Vol. 2018,
Issue. 11,
Dey, Parijat
Ghosh, Kausik
and
Sinha, Aninda
2018.
Simplifying large spin bootstrap in Mellin space.
Journal of High Energy Physics,
Vol. 2018,
Issue. 1,
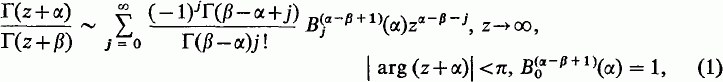
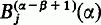 are the generalised Bernoulli polynomials, see (2), defined by
are the generalised Bernoulli polynomials, see (2), defined by


