Article contents
A note on some peculiar nonlinear extremal phenomena of the Chebyshev polynomials
Published online by Cambridge University Press: 20 January 2009
Abstract
We consider the problem of maximizing the sum of squares of the leading coefficients of polynomials 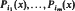 (where Pj(x) is a polynomial of degree j) under the restriction that the sup-norm of
(where Pj(x) is a polynomial of degree j) under the restriction that the sup-norm of 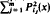 is bounded on the interval [ −b, b] (b>0). A complete solution of the problem is presented using duality theory of convex analysis and the theory of canonical moments. It turns out, that contrary to many other extremal problems the structure of the solution will depend heavily on the size of the interval [ −b, b].
is bounded on the interval [ −b, b] (b>0). A complete solution of the problem is presented using duality theory of convex analysis and the theory of canonical moments. It turns out, that contrary to many other extremal problems the structure of the solution will depend heavily on the size of the interval [ −b, b].
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1995
References
REFERENCES
- 5
- Cited by


