No CrossRef data available.
Article contents
A note on pseudo-umbilical surfaces
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We follow the notations and basic equations of Chen (2). Let M be a surface immersed in an m-dimensional space form Rm(c) of curvature c = 1, 0 or −1. We choose a local field of orthonormal frames e1, …, em in Rm(c) such that, restricted to M, the vectors e1, e2 are tangent to M. Let ω1, …, ωm be the field of dual frames. Then the structure equations of Rm(c) are given by
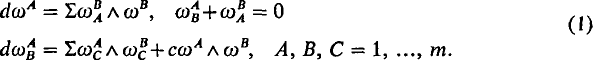
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 20 , Issue 2 , September 1976 , pp. 137 - 142
- Copyright
- Copyright © Edinburgh Mathematical Society 1976
References
REFERENCES
(2) Chen, B. Y., Pseudo-umbilical surfaces with constant Gauss curvature, Proc. Edinburgh Math. Soc. 18 (1972), 143–148.Google Scholar
(3) Chen, B. Y., Minimal surfaces with constant Gauss curvature, Proc. Amer. Math. Soc. 34 (1972), 504–508.CrossRefGoogle Scholar
(4) Moore, J. D., Isometric immersions of riemannian products. J. Diff. Geometry 5 (1971), 159–168.Google Scholar


