Article contents
A Note on Griffith Cracks†
Published online by Cambridge University Press: 20 January 2009
Extract
The problem of determining the distribution of stress in the neighbourhood of a Griffith crack, denned by ∣x∣ ≦ 1, y = 0, which is subject to an internal pressure varying along the length of the crack has been solved by Sneddon and Elliott (3) and by England and Green (1). In the former paper a Fourier cosine method is used to arrive at a solution while in the latter paper the problem is reduced to an Abel integral equation by making use of integral representations of the complex potentials given in Green and Zerna (2). Neither paper deals with the calculation of the stress intensity factor
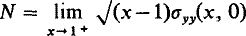
which is extremely important to workers in fracture mechanics.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 15 , Issue 2 , December 1966 , pp. 131 - 134
- Copyright
- Copyright © Edinburgh Mathematical Society 1966
References
REFERENCES
- 5
- Cited by


