Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T19:43:17.819Z Has data issue: false hasContentIssue false
  • English
  • Français

The normal vibrations of a rigid spherical punch on the surface of an elastic half-space

Published online by Cambridge University Press:  20 January 2009

R. J. M. Crozier  and
S. C. Hunter
R. J. M. Crozier
Affiliation:
Department of Mathematics, University of Strathclyde, Glasgow
S. C. Hunter
Affiliation:
Department of Mathematics, University of Strathclyde, Glasgow
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A rigid spherical punch vibrates normally on the surface of a semi-infinite isotropic elastic half-space. The essential novelty of this problem, which is treated within the context of classical elasticity, is that of a changing boundary; the radius of the circle of contact on the free surface varies with time. The geometrical co-ordinates are modified to yield a boundary value problem with fixed boundaries. However the governing differential equations become more complicated. These equations are solved by a perturbation procedure for the case where the contact radius a(t) is of the form

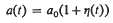
where a0 is constant and |ŋ(t)≪1. Finally the normal stress and the total load under the punch are evaluated in the form of series which are valid for sufficiently slowly varying ŋ(t).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 15 , Issue 4 , December 1967 , pp. 297 - 307
Copyright
Copyright © Edinburgh Mathematical Society 1967

References

REFERENCES

(1) Hunter, S. C., J. Mech. Phys. Sol. 8, (1960) 219.Google Scholar
(2) Hunter, S. C., J. Appl. Mechanics, 28 (1961), No. 4, 611.Google Scholar
(3) Green, A. E. and Zerna, W., Theoretical Elasticity (1954).Google Scholar
(4) Galin, L. A., Contact Problems in the Theory of Elasticity (1961), Translated from Russian by MrsMoss, H., ed. Sneddon, I. N., (North Carolina State College), NSF Grant No. G16447.Google Scholar
(5) Robertson, I. A., Proc. Camb. Phil. Soc. 62 (1966), 547.CrossRefGoogle Scholar