No CrossRef data available.
Article contents
Nonlinear periodic parabolic problems with nonmonotone discontinuities
Published online by Cambridge University Press: 20 January 2009
Abstract
In this paper we consider a nonlinear periodic parabolic boundary value problem with a discontinuous nonmonotone nonlinearity. Using a lifting result for operators of type (S+), a general surjectivity theorem for operators of monotone type and an auxiliary problem defined by truncation and penalization we prove the existence of a solution in the order interval formed by an upper and lower solution. Moreover we show that the set of all such solutions is compact in Lp(T, 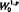 (Z)).
(Z)).
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 41 , Issue 1 , February 1998 , pp. 117 - 132
- Copyright
- Copyright © Edinburgh Mathematical Society 1998


