Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-03T19:14:59.537Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear boundary value problems for elliptic systems

Published online by Cambridge University Press:  20 January 2009

A. Cañada
A. Cañada
Affiliation:
Departamento de Analisis Matematico, Univeristy de Granada, 18071, Granada, Spain
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The purpose of this paper is to discuss non-linear boundary value problems for elliptic systems of the type

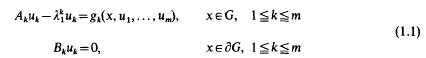
where Ak is a second order uniformly elliptic operator and 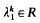is such that the problem

has a one-dimensional space of solutions that is generated by a non-negative function. The boundary ∂G is supposed to be smooth and the functions gk, 1≦k≦m are defined on Ḡ×Rm and are continuously differentiate (usually, Bk represents Dirichlet or Neumann conditions and 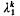is the first eigenvalue associated with Ak and such boundary conditions).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 30 , Issue 2 , June 1987 , pp. 257 - 272
Copyright
Copyright © Edinburgh Mathematical Society 1987

References

REFERENCES

1.Adams, R. A., Sobolev Spaces (Academic Press, 1975).Google Scholar
2.Agmon, S., Douglis, A. and Nirenberg, L., Estimates near the boundary for solutions of elliptic partial differential equations satisfying general boundary conditions, I, Comm. Pure Appl. Math. 12 (1959), 623–727.CrossRefGoogle Scholar
3.Brezis, H. and Strauss, W. A., Semilinear second order elliptic equations in L 1, J. Math. Soc. Japan 25 (1973), 565–590.CrossRefGoogle Scholar
4.Cañada, A. and Martinez-Amores, P., Solvability of some operator equations and periodic solutions of nonlinear functional differential equations, J. Differential Equations 49(3) (1983), 415–429.CrossRefGoogle Scholar
5.Cañada, A. and Ortega, R., Existence theorems for equations in normed spaces and boundary value problems for nonlinear vector ordinary differential equations, Proc. Royal Soc. Edinburgh 98A (1984), 1–11.CrossRefGoogle Scholar
6.Cañada, A., K-set contractions and nonlinear vector boundary value problems, J. Math. Anal. Appl. 117 (1) (1986), 1–22.CrossRefGoogle Scholar
7.De Figueiredo, D. G. and Ni, W., Perturbations of second order linear elliptic problems by nonlinearities without Landesman-Lazer condition, Nonlinear Anal. 3 (5) (1979), 295–307.CrossRefGoogle Scholar
8.Fraenkel, L. E., On the embedding of , J. London Math. Soc. (2) 26 (1982), 290–298.CrossRefGoogle Scholar
9.Fucik, S. and Kufner, A., Nonlinear Differential Equations (Elsevier, 1980).Google Scholar
10.Kazdan, L. J. and Warner, F. W., Remarks on some quasilinear elliptic equations, Comm. Pure Appl. Math. 28 (1975), 567–597.CrossRefGoogle Scholar
11.Landesman, E. M. and Lazer, A. C., Nonlinear perturbations of linear elliptic boundary value problems at resonance, J. Math. Mech. 19 (1970), 609–623.Google Scholar
12.Mawhin, L., Problémes aux limites du type de Neumann pour certaines equations différentielles on aux dérivées partielles non linéaires, in Equations differentielles el fonctionnelles non lineaires (Herman, 1973), 124–134.Google Scholar
13.Mawhin, J., Topological degree methods in nonlinear boundary value problems, Amer. Math. Soc. Reg. Conf. in Math. 40 (1979).Google Scholar
14.Rouche, N. and Mawhin, J., Equations differentielles ordinaires, Vol. II (Masson, 1973).Google Scholar