Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T07:15:43.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Newman's identities, lucas sequences and congruences for certain partition functions

Part of: Additive number theory; partitions Combinatorics

Published online by Cambridge University Press:  08 October 2020

Ernest X.W. Xia
Ernest X.W. Xia*
Affiliation:
Department of Mathematics, Jiangsu University, Zhenjiang, Jiangsu, 212013, P. R. China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let r be an integer with 2 ≤ r ≤ 24 and let pr(n) be defined by 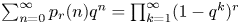$\sum _{n=0}^\infty p_r(n) q^n = \prod _{k=1}^\infty (1-q^k)^r$. In this paper, we provide uniform methods for discovering infinite families of congruences and strange congruences for pr(n) by using some identities on pr(n) due to Newman. As applications, we establish many infinite families of congruences and strange congruences for certain partition functions, such as Andrews's smallest parts function, the coefficients of Ramanujan's ϕ function and p-regular partition functions. For example, we prove that for n ≥ 0,

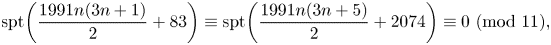\[ \textrm{spt}\bigg( \frac{1991n(3n+1) }{2} +83\bigg) \equiv \textrm{spt}\bigg(\frac{1991n(3n+5)}{2} +2074\bigg) \equiv 0\ (\textrm{mod} \ 11), \]
and for k ≥ 0,
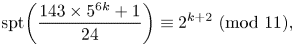\[ \textrm{spt}\bigg( \frac{143\times 5^{6k} +1 }{24}\bigg)\equiv 2^{k+2} \ (\textrm{mod}\ 11), \]
 where spt(n) denotes Andrews's smallest parts function.

Keywords

congruencespartitionsNewman's identitiesrankLucas sequences

MSC classification

Primary: 11P83: Partitions; congruences and congruential restrictions
Secondary: 05A17: Partitions of integers
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 63 , Issue 3 , August 2020 , pp. 709 - 736
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, G. E., The number of smallest parts in the partitions of n, J. Reine Angew. Math. 624 (2008), 133–142.Google Scholar
Chan, S. H., Congruences for Ramanujan's ϕ function, Acta Arith. 153 (2012), 161–189.CrossRefGoogle Scholar
Cui, S. P., Gu, S. S. and Huang, A. X., Congruence properties for a certain kind of partition functions, Adv. Math. 290 (2016), 739–772.CrossRefGoogle Scholar
Garvan, F., Congruences for Andrews’ smallest parts partition function and new congruences for Dyson's rank, Int. J. Number Theory 6 (2010), 281–309.CrossRefGoogle Scholar
Garvan, F., Congruences for Andrews’ spt-function modulo powers of 5, 7 and 13, Trans. Amer. Math. Soc. 364 (2012), 4847–4873.CrossRefGoogle Scholar
Hirschhorn, M. D. and Sellers, J. A., Arithmetic properties of partitions with odd parts distinct, Ramanujan J. 22 (2010), 273–284.CrossRefGoogle Scholar
Keith, W. J., Congruences for 9-regular partitions modulo 3, Ramanujan J. 35 (2014), 157–164.CrossRefGoogle Scholar
Lucas, E., Théorie des fonctions numériques simplement périodiques, Amer. J. Math. 1 (1878), 184–240.CrossRefGoogle Scholar
Newman, M., Remarks on some modular identities, Trans. Amer. Math. Soc. 73 (1952), 313–320.CrossRefGoogle Scholar
Newman, M., Further identities and congruences for the coefficients of modular forms, Canad. J. Math. 10 (1958), 577–586.CrossRefGoogle Scholar
Renault, M., The period, rank, and order of the (a, b)-Fibonacci sequence mod m, Math. Magazine 86 (2013), 372–380.CrossRefGoogle Scholar
Yao, O. X. M., New congruences modulo powers of 2 and 3 for 9-regular partitions, J. Number Theory 142 (2014), 89–101.CrossRefGoogle Scholar