No CrossRef data available.
Article contents
N-ary Transformations of Sequences
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let T(α1, α2, …, αn−1) be the n-ary transformation which takes the sequence {si}, (i = 0, 1, …), into the sequence {s'i} where
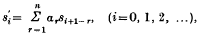
with sm = 0 when m is a negative integer, and where α1, …, αn an are real numbers with sum unity. In a previous note (1) conditions were found on α and β for the ternary transformation T(α, β) to be equivalent to convergence. A method is given here for treating the similar problem for the general n-ary transformation.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 11 , Issue 4 , November 1959 , pp. 221 - 222
- Copyright
- Copyright © Edinburgh Mathematical Society 1959
References
REFERENCES
Borwein, D. and Boyd, A. V., Binary and ternary transformations of sequences, Proc. Edin. Math. Soc, 11 (1959), 175–181.CrossRefGoogle Scholar


