Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T01:05:15.994Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplicity of solutions to the weighted critical quasilinear problems

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  04 January 2012

Sihua Liang  and
Jihui Zhang
Sihua Liang
Affiliation:
Department of Mathematics, Changchun Normal University, Changchun 130032, Jilin, People's Republic of China ([email protected])
Jihui Zhang
Affiliation:
Institute of Mathematics, School of Mathematical Science, Nanjing Normal University, Nanjing, Jiangsu 210046, People's Republic of China
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a class of critical quasilinear problems

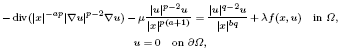
where 0 ∈ Ω ⊂ ℝN, N ≥ 3, is a bounded domain and 1 < p < N, a < N/p, a ≤ b < a + 1, λ is a positive parameter, 0 ≤ μ < 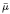≡ ((N − p)/p − a)p, q = q*(a, b) ≡ Np/[N − pd] and d ≡ a+1 − b. Infinitely many small solutions are obtained by using a version of the symmetric Mountain Pass Theorem and a variant of the concentration-compactness principle. We deal with a problem that extends some results involving singularities not only in the nonlinearities but also in the operator.

Keywords

degenerate quasilinear equationp-Laplacian operatorvariational methodsconcentration-compactness principle

MSC classification

Secondary: 35J60: Nonlinear elliptic equations 35B33: Critical exponents 35J65: Nonlinear boundary value problems for linear elliptic equations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 55 , Issue 1 , February 2012 , pp. 181 - 195
Copyright
Copyright © Edinburgh Mathematical Society 2011

References

1.Assunção, R. B., Carrião, P. C. and Miyagaki, O. H., Multiplicity of solutions for critical singular problems, Appl. Math. Lett. 19 (2006), 741–746.CrossRefGoogle Scholar
2.Assunção, R. B., Carrião, P. C. and Miyagaki, O. H., Critical singular problems via concentration-compactness lemma, J. Math. Analysis Applic. 326 (2007), 137–154.CrossRefGoogle Scholar
3.Assunção, R. B., Carrião, P. C. and Miyagaki, O. H., Subcritical perturbations of a singular quasilinear elliptic equation involving the critical Hardy–Sobolev exponent, Nonlin. Analysis 66 (2007), 1351–1364.CrossRefGoogle Scholar
4.Brézis, H. and Lieb, E., A relation between pointwise convergence of functions and convergence of functionals, Proc. Am. Math. Soc. 88 (1983), 486–490.CrossRefGoogle Scholar
5.Brézis, H. and Nirenberg, L., Positive solutions of nonlinear elliptic equations involving critical exponents, Commun. Pure Appl. Math. 34 (1983), 437–477.CrossRefGoogle Scholar
6.Caffarelli, L., Kohn, R. and Nirenberg, L., First order interpolation inequalities with weights, Compositio Math. 53(3) (1984), 259–275.Google Scholar
7.Cao, D. and Han, P., Solutions for semilinear elliptic equations with critical exponents and Hardy potential, J. Diff. Eqns 205 (2004), 521–537.CrossRefGoogle Scholar
8.Cao, D. and Han, P., Solutions to critical elliptic equations with multi-singular inverse square potentials, J. Diff. Eqns 224 (2006), 332–372.CrossRefGoogle Scholar
9.Cao, D. and Peng, S., A note on the sign-changing solutions to elliptic problems with critical Sobolev and Hardy terms, J. Diff. Eqns 193 (2003), 424–434.CrossRefGoogle Scholar
10.Chabrowski, J., On multiple solutions for the nonhomogeneous p-Laplacian with a critical Sobolev exponent, Diff. Integ. Eqns 8 (1995) 705–716.Google Scholar
11.Chen, J. and Li, S., On multiple solutions of a singular quasi-linear equation on unbounded domain, J. Math. Analysis Applic. 275 (2002), 733–746.CrossRefGoogle Scholar
12.Ferrero, A. and Gazzola, F., Existence of solutions for singular critical growth semilinear elliptic equations, J. Diff. Eqns 177 (2001), 494–522.CrossRefGoogle Scholar
13.Filippucci, R., Pucci, P. and Robert, F., On a p-Laplace equation with multiple critical nonlinearities, J. Math. Pures Appl. 91 (2009), 156–177.CrossRefGoogle Scholar
14.Ghoussoub, N. and Yuan, C., Multiple solutions for quasi-linear PDEs involving the critical Sobolev and Hardy exponents, Trans. Am. Math. Soc. 352 (2000), 5703–5743.CrossRefGoogle Scholar
15.He, X. M. and Zou, W. M., Infinitely many arbitrarily small solutions for singular elliptic problems with critical Sobolev-Hardy exponents, Proc. Edinb. Math. Soc. 52 (2009), 97–108.CrossRefGoogle Scholar
16.Horiuchi, T., Best constant in weighted Sobolev inequality with weights being powers of distance from the origin, J. Inequal. Applicat. 1 (1997), 275–292.Google Scholar
17.Huang, L., Wu, X. and Tang, C., Existence and multiplicity of solutions for semilinear elliptic equations with critical weighted Hardy–Sobolev exponents, Nonlin. Analysis 71 (2009), 1916–1924.CrossRefGoogle Scholar
18.Kajikiya, R., A critical-point theorem related to the symmetric mountain pass lemma and its applications to elliptic equations, J. Funct. Analysis 225 (2005), 352–370.CrossRefGoogle Scholar
19.Kang, D., Positive solutions to the weighted critical quasilinear problems, Appl. Math. Computat. 213 (2009), 432–439.CrossRefGoogle Scholar
20.Li, S. and Zou, W., Remarks on a class of elliptic problems with critical exponents, Nonlin. Analysis 32 (1998), 769–774.Google Scholar
21.Lions, P. L., The concentration-compactness principle in the caculus of variations: the limit case, I, Rev. Mat. Ibero. 1 (1985), 45–120.CrossRefGoogle Scholar
22.Lions, P. L., The concentration-compactness principle in the caculus of variations: the limit case, II, Rev. Mat. Ibero. 1 (1985), 145–201.CrossRefGoogle Scholar
23.Musina, R., Existence and multiplicity results for a weighted p-Laplace equation involving Hardy potentials and critical nonlinearities, Rend. Lincei Mat. Appl. 20 (2009), 127–143.Google Scholar
24.Secchi, S., Smets, D. and Willem, M., Remarks on a Hardy–Sobolev inequality, C. R. Acad. Sci. Paris 336 (2003), 811–815.CrossRefGoogle Scholar
25.Silva, E. A. and Xavier, M. S., Multiplicity of solutions for quasilinear elliptic problems involving critical Sobolev exponents, Annales Inst. H. Poincaré Analyse Non Linéaire 20 (2003), 341–358.CrossRefGoogle Scholar
26.Smets, D., A concentration-compactness principle lemma with applications to singular eigenvalue problems, J. Funct. Analysis 167 (1999), 463–480.CrossRefGoogle Scholar
27.Talenti, G., Best constant in Sobolev inequality, Annali Mat. Pura Appl. 110 (1976), 353–372.CrossRefGoogle Scholar
28.Terracini, S., On positive entire solutions to a class of equations with a singular coefficient and critical exponent, Adv. Diff. Eqns 2 (1996), 241–264.Google Scholar
29.Xuan, B., The solvability of quasilinear Brézis–Nirenberg-type problems with singular weights, Nonlin. Analysis 62 (2005), 703–725.CrossRefGoogle Scholar
30.Yang, M. and Shen, Z., The effect of domain topology on the number of positive solutions for singular elliptic problems involving the Caffarelli–Kohn–Nirenberg inequalities, J. Math. Analysis Applic. 334 (2007), 273–288.CrossRefGoogle Scholar