Hostname: page-component-5cf477f64f-pw477 Total loading time: 0 Render date: 2025-04-07T22:33:11.487Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple Solutions of Sublinear Quasilinear Schrödinger Equations with Small Perturbations

Part of: Equations of mathematical physics and other areas of application Elliptic equations and systems

Published online by Cambridge University Press:  29 November 2018

Liang Zhang ,
X. H. Tang  and
Yi Chen
Liang Zhang*
Affiliation:
School of Mathematical Sciences, University of Jinan, Jinan, Shandong 250022, People's Republic of China ([email protected])
X. H. Tang
Affiliation:
School of Mathematics and Statistics, Central South University, Changsha, Hunan 410083, People's Republic of China ([email protected])
Yi Chen
Affiliation:
Department of Mathematics, China University of Mining and Technology, Xuzhou 221116, People's Republic of China ([email protected])
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the existence of multiple solutions for the quasilinear Schrödinger equation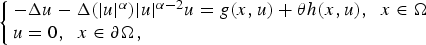

$$\left\{ {\matrix{ {-\Delta u-\Delta (\vert u \vert ^\alpha )\vert u \vert ^{\alpha -2}u = g(x,u) + \theta h(x,u),\;\;x\in \Omega } \hfill \cr {u = 0,\;\;x\in \partial \Omega ,} \hfill \cr } } \right.$$
where Ω is a bounded smooth domain in ℝN (N ≥ 1), α ≥ 2 and θ is a parameter. Under the assumption that g(x, u) is sublinear near the origin with respect to u, we study the effect of the perturbation term h(x, u), which may break the symmetry of the associated energy functional. With the aid of critical point theory and the truncation method, we show that this system possesses multiple small negative energy solutions.

Keywords

quasilinear Schrödinger equationsmultiple solutionscritical point theory

MSC classification

Primary: 35J20: Variational methods for second-order elliptic equations
Secondary: 35J65: Nonlinear boundary value problems for linear elliptic equations 35Q55: NLS-like equations (nonlinear Schrödinger)
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 62 , Issue 2 , May 2019 , pp. 471 - 488
Copyright
Copyright © Edinburgh Mathematical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Adachi, S. and Watanabe, T., Uniqueness of the ground state solutions of quasilinear Schrödinger equations, Nonlinear Anal. 75 (2012), 819–833.Google Scholar
2.Bartolo, R., Infinitely many solutions for quasilinear elliptic problems with broken symmetry, Adv. Nonlinear Stud. 13 (2013), 739–749.Google Scholar
3.Bolle, P., On the Bolza problem, J. Differential Equations 152 (1999), 274–288.Google Scholar
4.Candela, A. M., Palmieri, G. and Salvatore, A., Radial solutions of semilinear elliptic equations with broken symmetry, Topol. Methods Nonlinear Anal. 27 (2006), 117–132.Google Scholar
5.Chang, K. C., Methods in nonlinear analysis (Springer, 2005).Google Scholar
6.Colin, M. and Jeanjean, L., Solutions for a quasilinear Schrödinger equation, a dual approach, Nonlinear Anal. 56 (2004), 213–226.Google Scholar
7.do Ó, J., Miyagaki, O. and Soares, S., Soliton solutions for quasilinear Schrödinger equations with critical growth, J. Differential Equations 248 (2010), 722–744.Google Scholar
8.Dugundji, J., An extension of Tietze's theorem, Pacific J. Math. 1 (1951), 353–367.Google Scholar
9.Fang, X. D. and Szulkin, A., Multiple solutions for quasilinear Schrödinger equation, J. Differential Equations 254 (2013), 2015–2032.Google Scholar
10.Jing, Y. T. and Liu, Z. L., Infinitely many solutions of p-sublinear p-Laplacian equations, J. Math. Anal. Appl. 429 (2015), 1240–1257.Google Scholar
11.Kajikiya, R., Multiple solutions of sublinear Lane–Emden elliptic equations, Calc. Var. Partial Differential Equations 26 (2006), 29–48.Google Scholar
12.Kurihara, S., Large-amplitude quasi-solitons in superfluid films, J. Phys. Soc. Japan 50 (1981), 3262–3267.Google Scholar
13.Laedke, E. W., Spatschek, K. H. and Stenflo, L., Evolution theorem for a class of perturbed envelope soliton solutions, J. Math. Phys. 24 (1983), 2764–2769.Google Scholar
14.Li, Q. and Wu, X., Multiple solutions for generalized quasilinear Schrödinger equations, Math. Methods Appl. Sci. 40 (2017), 1359–1366.Google Scholar
15.Liu, J. Q. and Wang, Z. Q., Soliton solutions for quasilinear Schrödinger equations I, Proc. Amer. Math. Soc. 131 (2003), 441–448.Google Scholar
16.Liu, J. Q., Wang, Y. Q. and Wang, Z. Q., Soliton solutions for quasilinear Schrödinger equations II, J. Differential Equations 187 (2003), 473–493.Google Scholar
17.Liu, J. Q., Wang, Y. and Wang, Z. Q., Solutions for quasilinear Schrödinger equations via the Nehari method, Comm. Partial Differential Equations 29 (2004), 879–892.Google Scholar
18.Liu, X. Q., Liu, J. Q. and Wang, Z. Q., Quasilinear elliptic equations via perturbation method, Proc. Amer. Math. Soc. 141 (2013), 253–263.Google Scholar
19.Liu, X. Q. and Zhao, F. K., Existence of infinitely many solutions for quasilinear equations perturbed from symmetry, Adv. Nonlinear Stud. 13 (2013), 965–978.Google Scholar
20.Poppenberg, M., Schmitt, K. and Wang, Z. Q., On the existence of soliton solutions to quasilinear Schrödinger equations, Calc. Var. Partial Differential Equations 14 (2002), 329–344.Google Scholar
21.Rabinowitz, P., Minimax methods in critical point theory with applications to differential equations, CBMS, Volume 65 (American Mathematical Society, 1986).Google Scholar
22.Ritchie, B., Relativistic self-focusing and channel formation in laser-plasma interactions, Phys. Rev. E 50 (1994), 687–689.Google Scholar
23.Ruiz, D. and Siciliano, G., Existence of ground states for a modified nonlinear Schrödinger equation, Nonlinearity 23 (2010), 1221–1233.Google Scholar
24.Salvatore, A., Infinitely many solutions for symmetric and non-symmetric elliptic systems, J. Math. Anal. Appl. 336 (2010), 506–515.Google Scholar
25.Song, H. X., Chen, C. S. and Yan, Q. L., Infinitely many solutions for quasilinear Schrödinger equation with critical exponential growth in ℝN, J. Math. Anal. Appl. 439 (2016), 575–593.Google Scholar
26.Wu, X., Multiple solutions for quasilinear Schrödinger equations with a parameter, J. Differential Equations 256 (2014), 2619–2632.Google Scholar
27.Yue, X. R. and Zou, W. M., Infinitely many solutions for the perturbed Bose–Einstein condensates system, Nonlinear Anal. 94 (2014), 171–184.Google Scholar
28.Zhang, L. and Chen, Y., Infinitely many solutions for sublinear indefinite nonlocal elliptic equations perturbed from symmetry, Nonlinear Anal. 151 (2017), 126–144.Google Scholar
29.Zhang, L. and Tang, X. H., Perturbations from indefinite symmetric elliptic boundary value problems, Glasgow Math. J. 59 (2017), 635–648.Google Scholar
30.Zhang, L., Tang, X. H. and Chen, Y., Infinitely many solutions for quasilinear Schrödinger equations under broken symmetry situations, Topol. Methods Nonlinear Anal. 48 (2016), 539–554.Google Scholar
31.Zhang, L., Tang, X. H. and Chen, Y., Infinitely many solutions for indefinite quasilinear Schrödinger equations under broken symmetry situations, Math. Methods Appl. Sci. 40 (2017), 979–991.Google Scholar
32.Zhang, J., Tang, X. H. and Zhang, W., Existence of infinitely many solutions for a quasilinear elliptic equation, Appl. Math. Lett. 37 (2014), 131–135.Google Scholar
33.Zhou, F. and Wu, K., Infinitely many small solutions for a modified nonlinear Schrödinger equations, J. Math. Anal. Appl. 411 (2014), 953–959.Google Scholar