Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-29T01:20:36.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple solutions for a class of quasilinear problems with double criticality

Part of: Partial differential equations Linear function spaces and their duals Elliptic equations and systems

Published online by Cambridge University Press:  21 October 2022

Karima Ait-Mahiout ,
Claudianor O. Alves  and
Prashanta Garain
Karima Ait-Mahiout
Affiliation:
Laboratoire Théorie du point fixe et Applications, École Normale Supérieure, BP 92, Kouba 16006, Algeria ([email protected])
Claudianor O. Alves
Affiliation:
Unidade Acadêmica de Matemática, Universidade Federal de Campina Grande, 58429-970 Campina Grande, PB, Brazil ([email protected])
Prashanta Garain
Affiliation:
Department of Mathematics, Indian Institute of Technology Indore, Khandwa Road, Simrol, Madhya Pradesh 453552, India ([email protected]) Department of Mathematics, Ben-Gurion University of the Negev, P.O.B. 653, Beer Sheva 8410501, Israel, ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish multiplicity results for the following class of quasilinear problems P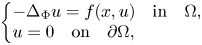

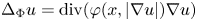\begin{equation*} \left\{ \begin{array}{@{}l} -\Delta_{\Phi}u=f(x,u) \quad \mbox{in} \quad \Omega, \\ u=0 \quad \mbox{on} \quad \partial \Omega, \end{array} \right. \end{equation*}
where $\Delta _{\Phi }u=\text {div}(\varphi (x,|\nabla u|)\nabla u)$ for a generalized N-function $\Phi (x,t)=\int _{0}^{|t|}\varphi (x,s)s\,ds$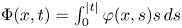. We consider $\Omega \subset \mathbb {R}^{N}$ 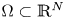to be a smooth bounded domain that contains two disjoint open regions $\Omega _N$ 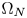and $\Omega _p$ 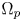such that $\overline {\Omega _N}\cap \overline {\Omega _p}=\emptyset$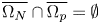. 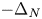The main feature of the problem $(P)$ is that the operator $-\Delta _{\Phi }$ behaves like $-\Delta _N$ on $\Omega _N$ 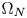and $-\Delta _p$ 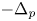on $\Omega _p$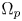. We assume the nonlinearity $f:\Omega \times \mathbb {R}\to \mathbb {R}$ 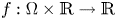of two different types, but both behave like $e^{\alpha |t|^{\frac {N}{N-1}}}$ 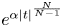on $\Omega _N$ 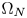and $|t|^{p^{*}-2}t$ 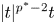on $\Omega _p$ 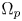as $|t|$ is large enough, for some $\alpha >0$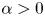 and $p^{*}=\frac {Np}{N-p}$ 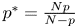being the critical Sobolev exponent for $1< p< N$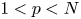. In this context, for one type of nonlinearity $f$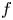, we provide a multiplicity of solutions in a general smooth bounded domain and for another type of nonlinearity $f$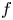, in an annular domain $\Omega$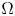, we establish existence of multiple solutions for the problem $(P)$ 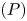that are non-radial and rotationally non-equivalent.

Keywords

variational methodsquasilinear problemsMusielak–Sobolev space

MSC classification

Primary: 35A15: Variational methods 35J62: Quasilinear elliptic equations 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.)
Secondary: 35B33: Critical exponents
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 4 , November 2022 , pp. 1011 - 1047
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Current address.

References

Adimurthi, A. and Yadava, S. L., Critical exponent problem in $\mathbb {R}^{2}$ with Neumann boundary condition, Comm. Partial Differ. Equ. 15(4) (1990), 461–501.CrossRefGoogle Scholar
Alves, C. O. and Barreiro, J. L. P., Existence and multiplicity of solutions for a $p(x)$-Laplacian equation with critical growth, J. Math. Anal. Appl. 403 (2013), 143–154.CrossRefGoogle Scholar
Alves, C. O. and Ferreira, M. C., Multi-bump solutions for a class of quasilinear problems involving variable exponents, Annali di Matematica 194 (2015), 1563–1593.CrossRefGoogle Scholar
Alves, C. O. and de Freitas, L. R., Multiplicity of nonradial solutions for a class of quasilinear equation on annulus with exponential critical growth, Top. Meth. Nonlinear Anal. 39 (2012), 243–262.Google Scholar
Alves, C. O. and Rădulescu, V., The Lane-Emden equation with variable double-phase and multiple regime, Proc. Amer. Math. Soc. 148 (2020), 2937–2952.CrossRefGoogle Scholar
Alves, C. O. and Souto, M. A. S., Existence of solutions for a class of problems in $\mathbb {R}^{N}$ involving the $p(x)$-Laplacian, Progr. Nonlinear Differ. Equ. Appl. 66 (2005), 17–32.Google Scholar
Alves, C. O., Figueiredo, G. M. and Santos, J. A., Strauss and Lions type results for a class of Orlicz-Sobolev spaces and applications, Topol. Methods Nonlinear Anal. 44 (2014), 435–456.CrossRefGoogle Scholar
Alves, C. O., Garain, P. and Rădulescu, V. D., High perturbations of quasilinear problems with double criticality, Math. Z. 299(3–4) (2021), 1875–1895.CrossRefGoogle Scholar
Ambrosetti, A. and Rabinowitz, P. H., Dual methods in critical point theory and applications, J. Funct. Anal. 14 (1973), 347–381.CrossRefGoogle Scholar
Azroul, E., Benkirane, A, Shimi, M. and Srati, M., Embedding and extension results in fractional Musielak-Sobolev spaces, e-print arXiv:2007.11043v1[Math AP].Google Scholar
Benkirane, A. and Sidi El Vally, M., An existence result for nonlinear elliptic equations in Musielak-Orlicz-Sobolev spaces, Bull. Belg. Math. Soc. 20(1) (2013), 1–187.Google Scholar
Bezerra do Ó, J. M., Medeiros, E. S. and Severo, U., On a quasilinear nonhomogeneous elliptic equation with critical growth in $\mathbb {R}^{N}$, J. Diff. Equ. 246 (2009), 1363–1386.CrossRefGoogle Scholar
Brezis, H. and Nirenberg, L., Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents, Comm. Pure Appl. Math. 36 (1983), 437–477.CrossRefGoogle Scholar
Byeon, J., Existence of many nonequivalent nonradial positive solutions of semilinear elliptic equations on three-dimensional annuli, J. Differ. Equ. 136 (1997), 136–165.CrossRefGoogle Scholar
Carvalho, M. L. M., Silva, E. D., Gonçalves, J. V. A. and Goulart, C., Critical elliptic problems using Concave-concave nonlinearities, Ann. Mat. Pura Appl. 198 (2019), 693–726.Google Scholar
Castro, A. and Finan, B. M., Existence of many positive nonradial solutions for a superlinear Dirichlet problem on thin annuli, Nonlinear Differ. Equ. 5 (2000), 21–31.Google Scholar
Catrina, F. and Wang, Z.-Q., Nonlinear elliptic equations on expanding symmetric domains, J. Differ. Equ. 156 (1999), 153–181.CrossRefGoogle Scholar
Chabrowski, J. and Fu, Y., Existence of solutions for $p(x)$-Laplacian problems on a bounded domain, J. Math. Anal. Appl 306 (2005), 604–618.CrossRefGoogle Scholar
Cherrier, P., Meilleures constantes dans les inegalites relatives aux espaces de Sobolev, Bull. Sci. Math. 108 (1984), 225–262.Google Scholar
Chlebicka, I., A pocket guide to nonlinear differential equations in the Musielak-Orlicz spaces, Nonlinear Anal. 175 (2018), 1–27.CrossRefGoogle Scholar
Cianchi, A., Moser-Trudinger inequalities without boundary conditions and isoperimetric problems, Indiana Univ. Math. J. 54 (2004), 669–706.CrossRefGoogle Scholar
Coffman, C., A non-linear boundary value problem with many positive solutions, J. Differ. Equ. 54 (1984), 429–437.CrossRefGoogle Scholar
Diening, L., Hästo, P., Harjulehto, P. and Ruzicka, M., Lebesgue and Sobolev spaces with variable exponents, Springer Lecture Notes, Volume 2017 (Springer-Verlag, Berlin, 2011).Google Scholar
de Figueiredo, D. G. and Miyagaki, O. H., Multiplicity of non-radial solutions of critical elliptic problems in an annulus, Proc. Roy. Soc. Edinburgh Sect. A 135 (2005), 25–37.CrossRefGoogle Scholar
Fan, X. L., On the sub-supersolution method for p(x)-Laplacian equations, J. Math. Anal. Appl. 330 (2007), 665–682.CrossRefGoogle Scholar
Fan, X. L., Differential equations of divergence form in Musielak-Sobolev spaces and a sub-supersolution method, J. Math. Anal. Appl. 386 (2012), 593–604.CrossRefGoogle Scholar
Fan, X. L. and Zhang, Q. H., Existence of solutions for $p(x)$-Laplacian Dirichlet problem, Nonlinear Anal. 52 (2003), 1843–1852.CrossRefGoogle Scholar
Fukagai, N. and Narukawa, K., On the existence of multiple positive solutions of quasilinear elliptic eigenvalue problems, Ann. Mat. Pura Appl. 186 186 (2007), 539–564.CrossRefGoogle Scholar
Fukagai, N., Ito, M. and Narukawa, K., Positive solutions of quasilinear elliptic equations with critical Orlicz-Sobolev nonlinearity on $\mathbb {R}^{N}$, Funkcial. Ekvac. 49 (2006), 235–267.CrossRefGoogle Scholar
Garcia Azorero, J. and Peral Alonso, I., Multiplicity of solutions for elliptic problems with critical exponent or with a nonsymmetric term, Trans. Amer. Math. Soc. 2 (1991), 877–895.CrossRefGoogle Scholar
Gossez, J., Nonlinear elliptic boundary value problems for equations with rapidly (or slowly) increasing coefficients, Trans. Amer. Math. Soc. 190 (1974), 163–205.CrossRefGoogle Scholar
Harjulehto, P. and Hästö, P., Orlicz spaces and generalized Orlicz spaces (Springer, 2019).CrossRefGoogle Scholar
Hirano, N. and Mizoguchi, N., Nonradial solutions of semilinear elliptic equations on annuli, J. Math. Soc. Japan 46 (1994), 111–117.CrossRefGoogle Scholar
Hudzik, H., On generalized Orlicz-Sobolev space, Funct. Approx. Comment. Math. 4 (1976), 37–51.Google Scholar
Kavian, O., Introduction à la Théorie Des Points Critiques: Et Applications Aux Problèmes Elliptiques (Springer, Heildelberg, 1993).Google Scholar
Kaur, B. S. and Sreenadh, K., Multiple positive solutions for a quasilinear elliptic equation with critical exponential nonlinearity, Nonlinear Anal. 73 (2010), 2368–2382.CrossRefGoogle Scholar
Kováčik, O. and Rákosník, J., On spaces $L^{p}(x)$ and $W^{k} p(x)$, Czech. Math. J. 41 (1991), 592–618.CrossRefGoogle Scholar
Li, Y. Y., Existence of many positive solutions of semilinear elliptic equations on annulus, J. Differ. Equ. 83 (1990), 348–367.CrossRefGoogle Scholar
Lin, S. S., Existence of many positive nonradial solutions for nonlinear elliptic equations on an annulus, J. Differ. Equ. 103 (1993), 338–349.CrossRefGoogle Scholar
Liu, D. and Zhao, P., Solutions for a quasilinear elliptic equation in Musielak-Sobolev spaces, Nonlinear Anal.: Real World Appl. 26 (2015), 315–329.CrossRefGoogle Scholar
de Medeiros, E. S., Existência e concentração de solução para o p-Laplaciano com condição de Neumann, Doctoral Dissertation, UNICAMP, 2001.Google Scholar
Mizoguchi, N. and Suzuki, T., Semilinear elliptic equations on annuli in three and higher dimensions, Houston J. Math. 22 (1996), 199–215.Google Scholar
Musielak, J., Orlicz spaces and modular spaces, Lecture Notes in Mathematics, Volume 1034 (Springer-Verlag, Berlin, 1983).Google Scholar
Pick, L., Kufner, A., John, O. and Fučík, S., Function spaces, Vol. 1, 2nd Revised and Extended Edition (De Gruyter, 2013).Google Scholar
Rabinowitz, P. H., Minimax methods in critical point theory with applications to differential equations, Volume 65 of CBMS Regional Conference Series in Mathematics. Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society (Providence, RI, 1986).CrossRefGoogle Scholar
Rădulescu, V. D. and Repovš, D. D., Partial differential equations with variable exponents: variational methods and qualitative analysis (CRC Press, Taylor & Francis Group, Boca Raton, FL, 2015).CrossRefGoogle Scholar
Silva, E. A. B. and Xavier, M. S., Multiplicity of solutions for quasilinear elliptic problems involving critical Sobolev exponents, Ann. Inst. H. Poincaré Anal. Non Linéaire 20(2) (2003), 341–358.CrossRefGoogle Scholar
Squassina, M., On Palais’ principle for non-smooth functionals, Nonlinear Anal. 74 (2011), 3786–3804.CrossRefGoogle Scholar
Struwe, M., Variational Methods (Springer-Verlag, Berlin, 1990).CrossRefGoogle Scholar
Suzuki, T., Positive solutions for semilinear elliptic equations on expanding annului: mountain pass approach, Funkcial. Ekvac. 39 (1996), 143–164.Google Scholar
Wang, L. and Liu, D., On a compact trace embedding theorem in Musielak-Sobolev spaces arXiv:1911.10331v1[Math.FA], November 23, 2019.Google Scholar
Wang, Z. and Willem, M., Existence of many positive solutions of semilinear elliptic equations on an annulus, Proc. Amer. Math. Soc. 127 (1999), 1711–1714.CrossRefGoogle Scholar
Wei, Z. H. and Wu, X. M., A multiplicity result for quasilinear elliptic equations involving critical Sobolev exponents, Nonlinear Anal. 18(6) (1992), 559–567.Google Scholar
Willem, M., Minimax theorems (Birkhäuser Boston Inc., Boston, MA, 1996).CrossRefGoogle Scholar