Article contents
The Motion of a Flat Plate from Rest in a Visco-elastic Liquid
Published online by Cambridge University Press: 20 January 2009
Extract
Oldroyd (1) considered non-Newtonian liquids for which the stress tensor sik and the rate of strain tensor eik=½(υk,i+υi,k)are related as follows
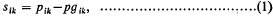
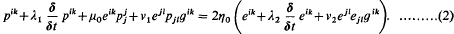
Here υi denotes the velocity vector, p an isotropic pressure, gik the metric tensor, and t time; η0 is a constant having the dimensions of viscosity and λ1, λ2, μ0, ν1, ν2, are constants having the dimension of time. Covariant suffixes are written below, contravariant above and the usual summation convention is employed. A suffix i following a comma indicates covariant differentiation with respect to the space variable xi.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1963
References
REFERENCES
- 3
- Cited by


