No CrossRef data available.
Article contents
The Modified Bessel Function Kn(z)
Published online by Cambridge University Press: 20 January 2009
Extract
Gray and Mathews, in their treatise on Bessel Functions, define the function Kn(z) to be
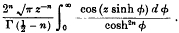
We shall denote this function by Vn(z). This definition only holds when z is real, and R(n)≧0. The asymptotic expansion of the function is also given; but the proof, which is said to be troublesome and not very satisfactory, is omitted. Basset (Proc. Camb. Phil. Soc., Vol. 6) gives a similar definition of the function.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1919
References
* Of. Maodonald, , Proc. London Math. Soc., XXX.Google Scholar
* Cf. MacRobert's, Functions of a Complex Variable, p. 239.Google Scholar
† Cf. Whittaker, and Watson, , Analysis, p. 376.Google Scholar
* Cf. Fourier, , Théorie Analytique de la Chaleur, Ch. VI.Google Scholar, Gray & Mathews, Ch. V., and Clifford, , Mathematical Papers, p. 346.Google Scholar
* Cf. Macdonald, , Proc. London Math. Soc., XXX.Google Scholar
* Kugelfunctionen, p. 237.
* Cf. Macdonald, , Proc. London Math. Soc., XXX., p. 170Google Scholar, and Hardy, , Quarterly Journal, XXXIX.Google Scholar
* Cf. Whittaker, and Watson, , Analysis, Chapter XVI.Google Scholar


