Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hillman, Jonathan A.
2021.
2019-20 MATRIX Annals.
Vol. 4,
Issue. ,
p.
57.


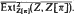 Similarly, if π is a PD
Similarly, if π is a PD