Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T12:38:42.347Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean values of multiplicative functions and applications to residue-class distribution

Part of: Elementary number theory Multiplicative number theory

Published online by Cambridge University Press:  10 February 2025

Paul Pollack  and
Akash Singha Roy
Paul Pollack*
Affiliation:
Department of Mathematics, University of Georgia, Athens, GA, USA
Akash Singha Roy
Affiliation:
Department of Mathematics, University of Georgia, Athens, GA, USA
*
Corresponding author: Paul Pollack, email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide a uniform bound on the partial sums of multiplicative functions under very general hypotheses. As an application, we give a nearly optimal estimate for the count of 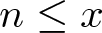$n \le x$ for which the Alladi–Erdős function 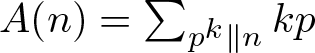$A(n) = \sum_{p^k \parallel n} k p$ takes values in a given residue class modulo q, where q varies uniformly up to a fixed power of $\log x$. We establish a similar result for the equidistribution of the Euler totient function 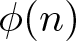$\phi(n)$ among the coprime residues to the ‘correct’ moduli q that vary uniformly in a similar range and also quantify the failure of equidistribution of the values of 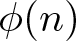$\phi(n)$ among the coprime residue classes to the ‘incorrect’ moduli.

Keywords

multiplicative functionmean valuesequidistributionuniform distributionweak equidistributionweak uniform distributionAlladi–Erdős functionEuler totient function

MSC classification

Primary: 11A25: Arithmetic functions; related numbers; inversion formulas
Secondary: 11N36: Applications of sieve methods 11N64: Other results on the distribution of values or the characterization of arithmetic functions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alladi, K. and Erdos, P., On an additive arithmetic function, Pacific J. Math. 71(2) (1977), 275–294.CrossRefGoogle Scholar
Balasuriya, S., Shparlinski, I. E. and Sutantyo, D., Multiplicative character sums with the Euler function, Studia Sci. Math. Hungar. 46(2) (2009), 223–229.Google Scholar
Banks, W. D. and Shparlinski, I. E., Congruences and exponential sums with the Euler function, High primes and misdemeanours: lectures in honour of the 60th birthday of Hugh Cowie Williams. Fields Inst. Commun., Volume41, (Amer. Math. Soc, Providence, RI, 2004).Google Scholar
Banks, W. D. and Shparlinski, I. E., Congruences and rational exponential sums with the Euler function, Rocky Mountain J. Math. 36(5) (2006), 1415–1426.CrossRefGoogle Scholar
De Koninck, J. M. and Kátai, I., On the local distribution of certain arithmetic functions, Liet. Mat. Rink. 46(3) (2006), 315–331. MR 2285346.Google Scholar
Delange, H., On integral-valued additive functions, J. Number Theory 1 (1969), 419–430.CrossRefGoogle Scholar
Dence, T. and Pomerance, C., Euler’s function in residue classes. Ramanujan J., 2(1-2) (1998), (Paul Erdős, 1913–1996), 7–20.Google Scholar
Goldfeld, D., On an additive prime divisor function of Alladi and Erdős, Analytic number theory, modular forms and q-hypergeometric series. Springer Proc. Math. Stat., Volume221, (Springer, Cham, 2017).Google Scholar
Halász, G., Über die Mittelwerte multiplikativer zahlentheoretischer Funktionen, Acta Math. Acad. Sci. Hungar. 19 (1968), 365–403.CrossRefGoogle Scholar
Hall, R. R. and Tenenbaum, G. and Divisors, , Cambridge Tracts in Mathematics, Volume90, (Cambridge University Press, Cambridge, 1988).Google Scholar
Hall, R. R. & Tenenbaum, G.. Effective mean value estimates for complex multiplicative functions, Math. Proc. Cambridge Philos. Soc. 19 (1991), 337–351CrossRefGoogle Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, 6th edn, (Oxford University Press, Oxford, 2008).CrossRefGoogle Scholar
Kátai, I., On the average prime divisors, Ann. Univ. Sci. Budapest. Sect. Comput. 27 (2007), 137–144, MR 2388547.Google Scholar
Lebowitz-Lockard, N., Pollack, P. and Singha Roy, A., Distribution mod p of Euler’s totient and the sum of proper divisors, Michigan Math. J. 74(1) (2024), 143–166. doi:10.1307/mmj/20216082CrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative number theory. I. Classical theory. Cambridge Studies in Advanced Mathematics, Volume97, (Cambridge University Press, Cambridge, 2007).Google Scholar
Narkiewicz, W., On distribution of values of multiplicative functions in residue classes, Acta Arith 12 (1967), 269–279.CrossRefGoogle Scholar
Pollack, P. and Singha Roy, A., Joint distribution in residue classes of polynomial-like multiplicative functions, Acta Arith 202(1) (2022), 89–104.CrossRefGoogle Scholar
Pollack, P. and Singha Roy, A., Benford behavior and distribution in residue classes of large prime factors, Canad. Math. Bull. 66(2) (2023), 626–642.CrossRefGoogle Scholar
Pollack, P. and Singha Roy, A., Distribution in coprime residue classes of polynomially-defined multiplicative functions, Math. Z. 303(4) (2023), .CrossRefGoogle Scholar
Scourfield, E. J., Uniform estimates for certain multiplicative properties, Monatsh. Math. 97(3) (1984), 233–247.CrossRefGoogle Scholar
Scourfield, E. J., A uniform coprimality result for some arithmetic functions, J. Number Theory 20(3) (1985), 315–353.CrossRefGoogle Scholar
Singha Roy, A., Joint distribution in residue classes of families of polynomially-defined multiplicative functions I, submitted.Google Scholar
Singha Roy, A., Mean values of multiplicative functions and applications to the distribution of the sum of divisors, submitted.Google Scholar
Tenenbaum, G., Introduction to analytic and probabilistic number theory. Graduate Studies in Mathematics, 3rd, Vol. 163 (American Mathematical Society, Providence, RI, 2015).Google Scholar