Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Spira, Robert
1967.
Zeros of approximate functional approximations.
Mathematics of Computation,
Vol. 21,
Issue. 97,
p.
41.
Redheffer, R. M.
1967.
Bemerkungen über Differentialungleichungen bei abzählbaren Ausnahmemengen.
Numerische Mathematik,
Vol. 9,
Issue. 5,
p.
437.
Robertson, J. M.
1969.
A local mean value theorem for the complex plane.
Proceedings of the Edinburgh Mathematical Society,
Vol. 16,
Issue. 4,
p.
329.
NASHED, M.Z.
1971.
Nonlinear Functional Analysis and Applications.
p.
103.
TAPIA, R.A.
1971.
Nonlinear Functional Analysis and Applications.
p.
45.
Flett, T. M.
1972.
Mean value theorems for vector-valued functions.
Tohoku Mathematical Journal,
Vol. 24,
Issue. 2,
Goldstein, A. A.
1972.
A Note on the Mean Value Theorem.
The American Mathematical Monthly,
Vol. 79,
Issue. 1,
p.
51.
Morales, Pedro
1972.
Mean Value Theorem for the m-Integral of Dinculeanu.
Canadian Mathematical Bulletin,
Vol. 15,
Issue. 2,
p.
243.
Tapia, R. A.
1973.
A characterization of inner product spaces.
Proceedings of the American Mathematical Society,
Vol. 41,
Issue. 2,
p.
569.
Ortega, James M.
1973.
Stability of Difference Equations and Convergence of Iterative Processes.
SIAM Journal on Numerical Analysis,
Vol. 10,
Issue. 2,
p.
268.
Tapia, R. A.
1973.
A characterization of inner product spaces.
Bulletin of the American Mathematical Society,
Vol. 79,
Issue. 3,
p.
530.
Goldstein, A.A.
1975.
Nonlinear Programming 2.
p.
215.
Diaz, J. B.
and
Výborný, R.
1975.
Generalized mean value theorems of the differential calculus.
Journal of the Australian Mathematical Society,
Vol. 20,
Issue. 3,
p.
290.
Kelley, Walter G.
1976.
Periodic Solutions of Generalized Differential Equations.
SIAM Journal on Applied Mathematics,
Vol. 30,
Issue. 1,
p.
70.
Dayal, S.
1977.
A converse of Taylor’s theorem for functions on Banach spaces.
Proceedings of the American Mathematical Society,
Vol. 65,
Issue. 2,
p.
265.
Von Betten, Dieter
1979.
Komplexe Schiefparabel-Ebenen.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 48,
Issue. 1,
p.
76.
Hiriart-Urruty, J-B.
1980.
Mean value theorems in nonsmooth analysis.
Numerical Functional Analysis and Optimization,
Vol. 2,
Issue. 1,
p.
1.
Výborný, Rudolf
1981.
Mean value theorems and a Taylor theorem for vector valued functions.
Bulletin of the Australian Mathematical Society,
Vol. 24,
Issue. 1,
p.
69.
Johnston, Elgin H.
1983.
The mean value theorem and analytic functions.
Proceedings of the Edinburgh Mathematical Society,
Vol. 26,
Issue. 3,
p.
289.
Furi, M.
and
Martelli, M.
1991.
On the Mean Value Theorem, Inequality, and Inclusion.
The American Mathematical Monthly,
Vol. 98,
Issue. 9,
p.
840.



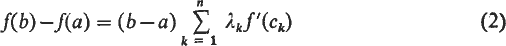
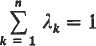 .
.