Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T11:21:24.786Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal functions and transference for groups of operators

Published online by Cambridge University Press:  20 January 2009

Gordon Blower
Gordon Blower
Affiliation:
Department of Mathematics and Statistics, Lancaster University, Lancaster LA1 4YF, UK
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Δ be the Laplace operator on ℝd and 1 < δ < 2. Using transference methods we show that, for max {q, q/(q – 1)} < 4d/(2d + 1 – δ), the maximal function 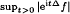for the Schrödinger group is in Lq, for f ∈ Lq with Δδ/2f ∈Lq. We obtain a similar result for the Airy group exp it Δ3/2. An abstract version of these results is obtained for bounded C0-groups eitL on subspaces of Lp spaces. Certain results extend to maximal functions defined for functions with values in U M D Banach spaces.

Keywords

transferenceoperator groupsSchrödinger equation
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 43 , Issue 1 , February 2000 , pp. 57 - 71
Copyright
Copyright © Edinburgh Mathematical Society 2000

References

1.Berkson, E. and Gillespie, T. A., Spectral decompositions and harmonic analysis on U M D spaces, Studia Math. 112 (1994), 13–49.Google Scholar
2.Berkson, E. and Gillespie, T. A., The q-variation of functions and spectral integration of Fourier multipliers, Duke Math. J. 88 (1997), 103–132.CrossRefGoogle Scholar
3.Berkson, E., Gillespie, T. A. and Muhly, P. S., Abstract spectral decompositions guaranteed by the Hilbert transform, Proc. Lond. Math. Soc. (3) 53 (1986), 489–517.CrossRefGoogle Scholar
4.Blower, G., Multipliers for semigroups, Proc. Edinb. Math. Soc. 39 (1996), 241–252.CrossRefGoogle Scholar
5.Bourgain, J., A remark on Schrödinger operators, Israel J. Math. 77 (1992), 1–16.CrossRefGoogle Scholar
6.Bourgain, J., Vector-valued singular integrals and the H1-BMO duality, in Probability theory and harmonic analysis (ed. Chao, J. A. and Woyczyński, W. A.), pp. 1–19 (Marcel Dekker, New York, 1986).Google Scholar
7.Carleson, L., Some analytic problems related to statistical mechanics, in Euclidean harmonic analysis (ed. Benedetto, J. J.), pp. 5–45, Lecture Notes in Mathematics, vol. 779 (Springer, Berlin, 1980).CrossRefGoogle Scholar
8.Chernoff, P. R., Essential self-adjointness of powers of generators of hyperbolic equations, J. Funct. Analysis 12 (1973), 401–414.CrossRefGoogle Scholar
9.Coifman, R., De Francia, J. L. R. and Semmes, S., Multiplicateurs de Fourier de Lp (ℝ) et estimations quadratiques, C. R. Acad. Sci. Paris Ser. 1 306 (1988), 351–4.Google Scholar
10.Cowling, M. G., Harmonic analysis on semigroups, Ann. Math. 117 (1983), 267–283.CrossRefGoogle Scholar
11.De Francia, J. L. R., A Littlewood–Paley inequality for arbitrary intervals, Rev. Mat. Iberoamericana 1 (1985), 1–14.CrossRefGoogle Scholar
12.Erdélyi, A., Asymptotic expansions (Dover, New York, 1955).CrossRefGoogle Scholar
13.Hille, E. and Phillips, R. S., Functional analysis and semi-groups, Colloquium Publications, vol. XXXI (AMS, Providence, RI, 1957).Google Scholar
14.Kwapień, S., Isomorphic characterizations of inner product spaces by orthogonal series with vector valued coefficients, Studia Math. 44 (1972), 583–595.CrossRefGoogle Scholar
15.Milman, V. D. and Schechtman, G., Asymptotic theory of finite-dimensional normed spaces, Lecture Notes in Mathematics, vol. 1200 (Springer, Berlin, 1986).Google Scholar
16.Stein, E. M., Singular integrals and differentiability properties of functions (Princeton University Press, Princeton, NJ, 1970).Google Scholar
17.Stein, E. M., Topics in harmonic analysis related to the Littlewood-Paley theory (Princeton University Press, Princeton, NJ, 1970).CrossRefGoogle Scholar
18.Stein, E. M., Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals (Princeton University Press, Princeton, NJ, 1993).Google Scholar
19.Wojtasczyck, P., Banach spaces for analysts (Cambridge University Press, 1989).Google Scholar
20.Xu, Q. H., Fourier multipliers for Lp(ℝn) via q-variation, Pacific J. Math. 176 (1996), 287–296.CrossRefGoogle Scholar
21.Zygmund, A., Trigonometric series, vol. 2 (Cambridge University Press, 1959).Google Scholar